
题目列表(包括答案和解析)
已知数列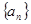 中,
中,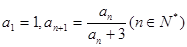
(Ⅰ)求证: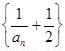 是等比数列,并求
是等比数列,并求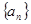 的通项公式
的通项公式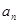 ;
;
(Ⅱ)数列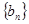 满足
满足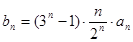 ,数列
,数列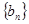 的前n项和为
的前n项和为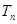 ,若不等式
,若不等式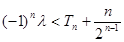 对一切
对一切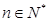 恒成立,求
恒成立,求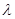 的取值范围。
的取值范围。
|
| lim |
| n→∞ |
| 1 |
| 96 |
|
1. 2.
2. 3.a=-2. 4.
3.a=-2. 4.  5.
5. 6.
6.
7. 8.
8. 9.
9. 10.
10. 11.
11. 12.0 13.
12.0 13. 14.18
14.18
15.解:(Ⅰ)由 得
得 ,
, ,
3分
,
3分
 ,
5分
,
5分
又 ,∴
,∴  。
7分
。
7分
(Ⅱ)由 可得,
可得, ,
9分
,
9分
由 得,
得, ,
12分
,
12分
所以,△ABC面积是 14分
14分
17.解:(Ⅰ)在Rt△ABC中,AB=1,
∠BAC=60°,∴BC= ,AC=2.
,AC=2.
在Rt△ACD中,AC=2,∠CAD=60°,
∴CD=2 ,AD=4.
,AD=4.
∴SABCD=

 .……………… 3分
.……………… 3分
则V= . ……………… 5分
. ……………… 5分
(Ⅱ)∵PA=CA,F为PC的中点,
∴AF⊥PC. ……………… 7分
∵PA⊥平面ABCD,∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.∴CD⊥PC.
∵E为PD中点,F为PC中点,
∴EF∥CD.则EF⊥PC. ……… 9分
∵AF∩EF=F,∴PC⊥平面AEF.…… 10分
(Ⅲ)证法一:
取AD中点M,连EM,CM.则EM∥PA.
∵EM  平面PAB,PA
平面PAB,PA 平面PAB,
平面PAB,
∴EM∥平面PAB. ……… 12分
在Rt△ACD中,∠CAD=60°,AC=AM=2,
∴∠ACM=60°.而∠BAC=60°,∴MC∥AB.
 ∵MC
∵MC  平面PAB,AB
平面PAB,AB 平面PAB,
平面PAB,
∴MC∥平面PAB. ……… 14分
∵EM∩MC=M,
∴平面EMC∥平面PAB.
∵EC 平面EMC,
平面EMC,
∴EC∥平面PAB. ……… 15分
证法二:
延长DC、AB,设它们交于点N,连PN.
∵∠NAC=∠DAC=60°,AC⊥CD,
∴C为ND的中点. ……12分
∵E为PD中点,∴EC∥PN.……14分
∵EC  平面PAB,PN
平面PAB,PN  平面PAB,
平面PAB,
∴EC∥平面PAB. ……… 15分
17.解:(Ⅰ)n≥2时, . ………………… 4分
. ………………… 4分
n=1时, ,适合上式,
,适合上式,
∴
 .
………………… 5分
.
………………… 5分
(Ⅱ) ,
, .
………………… 8分
.
………………… 8分
即 .
.
∴数列 是首项为4、公比为2的等比数列. ………………… 10分
是首项为4、公比为2的等比数列. ………………… 10分
 ,∴
,∴
 .……………… 12分
.……………… 12分
Tn= =
= .
………………… 14分
.
………………… 14分
18.解:(Ⅰ) …… 4分
…… 4分
= …………………… 8分
…………………… 8分
(Ⅱ)当0≤t<10时,y的取值范围是[1200,1225],
在t=5时,y取得最大值为1225; …………………… 11分
当10≤t≤20时,y的取值范围是[600,1200],
在t=20时,y取得最小值为600. …………………… 14分
(答)总之,第5天,日销售额y取得最大为1225元;
第20天,日销售额y取得最小为600元. …………………… 15分
19. 解:(Ⅰ)设圆心
 ,则
,则 ,解得
,解得 …………………(3分)
…………………(3分)
则圆 的方程为
的方程为 ,将点
,将点 的坐标代入得
的坐标代入得 ,故圆
,故圆 的方程为
的方程为
…………(5分)
(Ⅱ)设 ,则
,则 ,且
,且 …………………(7分)
…………………(7分)
= =
= ,所以
,所以 的最小值为
的最小值为 (可由线性规划或三角代换求得)
(可由线性规划或三角代换求得)
…………(10分)
(Ⅲ)由题意知, 直线 和直线
和直线 的斜率存在,且互为相反数,故可设
的斜率存在,且互为相反数,故可设 ,
,
 ,由
,由 ,得
,得
……………………(11分)
因为点 的横坐标
的横坐标 一定是该方程的解,故可得
一定是该方程的解,故可得 ………………………
………………………
(13分)
同理, ,所以
,所以 =
=
所以,直线 和
和 一定平行…………………………………………………………………(15分)
一定平行…………………………………………………………………(15分)
20.解:(Ⅰ) ,
, ,
, .
.
∴ ,且
,且 . …………………… 2分
. …………………… 2分
解得a=2,b=1. …………………… 4分
(Ⅱ) ,令
,令 ,
,
则 ,令
,令 ,得x=1(x=-1舍去).
,得x=1(x=-1舍去).
在 内,当x∈
内,当x∈ 时,
时, ,∴h(x)是增函数;
,∴h(x)是增函数;
当x∈ 时,
时, ,∴h(x)是减函数. …………………… 7分
,∴h(x)是减函数. …………………… 7分
则方程 在
在 内有两个不等实根的充要条件是
内有两个不等实根的充要条件是 ……10分
……10分
即 . …………………… 12分
. …………………… 12分
(Ⅲ) ,
, .
.
假设结论成立,则有
①-②,得 .
.
∴ .
.
由④得 ,
,
∴ .即
.即 .
.
即 .⑤
…………………… 14分
.⑤
…………………… 14分
令 ,
, (0<t<1),
(0<t<1),
则 >0.∴
>0.∴ 在0<t<1上增函数.
在0<t<1上增函数.
 ,∴⑤式不成立,与假设矛盾.
,∴⑤式不成立,与假设矛盾.
∴ .
……………………………16
.
……………………………16
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com