
题目列表(包括答案和解析)
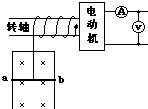 如图所示,电动机通过其转轴上的绝缘细绳竖直向上牵引一根原来静止的长为L=1m、质量m=O.1㎏的导体棒ab,导体棒紧贴在竖直放置、电阻不计的金属框架上,导体棒的电阻R=1Ω,磁感强度B=1T的匀强磁场方向垂直于导体框架所在平面,当导体棒在电动机牵引下上升h=3.8m时,获得稳定速度,此过程导体棒产生热量Q=2J.电动机工作时,输出功率P=6W恒定,不计一切摩擦,求:
如图所示,电动机通过其转轴上的绝缘细绳竖直向上牵引一根原来静止的长为L=1m、质量m=O.1㎏的导体棒ab,导体棒紧贴在竖直放置、电阻不计的金属框架上,导体棒的电阻R=1Ω,磁感强度B=1T的匀强磁场方向垂直于导体框架所在平面,当导体棒在电动机牵引下上升h=3.8m时,获得稳定速度,此过程导体棒产生热量Q=2J.电动机工作时,输出功率P=6W恒定,不计一切摩擦,求: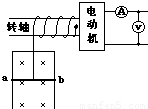
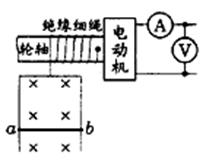
如图所示,电动机通过其转轴上的绝缘细绳牵引一根原来静止的长为L=1m,质量m=0.1㎏的导体棒ab,导体棒紧贴在竖直放置、电阻不计的金属框架上,导体棒的电阻R=1Ω,磁感强度B=1T的匀强磁场方向垂直于导体框架所在平面.当导体棒在电动机牵引下上升h=3.8m时,获得稳定速度,此过程中导体棒产生热量Q=2J.电动机工作时,电压表、电流表的读数分别为7V和1A,电动机的内阻r=1Ω.不计一切摩擦,g取10m/s2.求:
(1)导体棒所达到的稳定速度是多少?
(2)导体棒从静止到达稳定速度的时间是多少?

一.选择题
1.C
2.A
3.B
4.C
5.B
6.B
7.D
8.BD
9.ABD
10.AC
二.实验题(18分)
11.(1)C (3分)(2)AB(3分)
12.(1)D (2)C 保持R不阻值不变,调节R′阻值 DACB R» R′ 大 小
.files/image031.gif) |
三.计算题(52分)
13.滑沙者在斜面上下滑的过程中,受到重力mg、斜面对支持力N和摩擦力f,其中f=μN=μmgcos53°设其下滑过程中的加速度为a1,由牛顿第二定律
mgsin53°-μmgcos53°=ma1-------------------------------①
s=a1t12-----------------------------------------------------------②
v= a1t1--------------------------------------------------------------③
其中斜坡长度s= h/sin53°t1为滑沙者在斜坡上的滑行时间,v为其滑至坡底时的速度大小,由①②③式可解得
a1=
在水平沙滩上,滑沙者滑行的加速度为a2,由牛顿第二定律
μmg=ma2-----------------------------------------------------------④
设滑沙者在水平沙滩上又滑行了时间t2,由速度公式
0=v-a2 t2----------------------------------------------------------⑤
由④⑤式得 t2=7s
所以滑沙者总共滑行的时间t= t1 +t2=12s------------------⑥
本题共16分,其中①式4分,②③④⑤式各2分,⑥式4分(结果错误扣1分)。其他方法正确也给分。
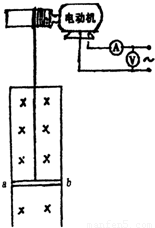
14.线框被匀速拉出磁场的过程中,受到竖直向下的重力mg、安培力F及竖直向上的绳的拉力FT,线框中产生的感应电动势、感应电流分别为E、I′。
由物体的平衡条件
FT=mg+F------------------------------------------------------------------①
其中 F=BI′L------------------------------------------------------------②
I′=E/R--------------------------------------------------------------------③
E=BLv---------------------------------------------------------------------④
由①②③④式可解得
FT=mg+------------------------------------------------------------⑤
设线框被匀速拉出磁场所用时间为t,由能量转化和守恒定律
UIt=FTvt+Q-----------------------------------------------------------------⑥
其中Q为电机线圈内阻产生的热量
t=L/v-----------------------------------------------------------------------⑦
解得Q=(UI-mgv-)-------------------------------------⑧
本题共16分,①②③④⑤⑥⑦⑧式各2分。其他方法正确也给分。
15.(1)设子弹、小物块、长木板的质量分别为m0、M、m,子弹的初速度为v0,子弹击中小物块后二者的共同速度为v1,由动量守恒定律
m0 v0=(M+ m0) v1-------------------------------------------------------------------------------①
子弹击中小物块后物块的质量为M′,且M′= M+ m0.设当物块滑至第n块木板时,木板才开始运动
μ
其中μ1、μ2分别表示物块与木板间、木板与地面间的动摩擦因数.
由式解得n>4.3
即物块滑上第五块木板时,木板才开始在地面上滑动.
(2)设物块刚滑上第五块木板时的速度为v2,每块木板的长度为L,由动能定理
-μ
由①②式解得 v2=
物块在第五块木板表面做匀减速直线运动,木板做匀加速直线运动,设经历时间t,物块与木板能获得相同的速度v3,由动量定理
-μ
〔μ1 M′g-μ2(M′+m)〕t=m v3--------------------------------------------------------------⑥
由⑤⑥式解得v3=m/s-----------------------------------------------------------------------⑦
在此过程中,物块发生的位移为s1,由动能定理
-μ
解得s1=m<
即物块与木板获得m/s的共同速度,之后整体向前匀减速运动s2后静止.
由动能定理
-μ2 (M′+m)g s2=-(M′+m)v32 ------------------------------------------------------⑨
解得s2=m
所以物块总共发生的位移s=
解得s≈
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com