
题目列表(包括答案和解析)
袋子中装有大小形状完全相同的m个红球和n个白球,其中m,n满足m>n≥2且m+n≤l0(m,n∈N+),若从中取出2个球,取出的2个球是同色的概率等于取出的2个球是异色的概率.
(Ⅰ) 求m,n的值;
(Ⅱ) 从袋子中任取3个球,设取到红球的个数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
【解析】第一问中利用 ,解得m=6,n=3.
,解得m=6,n=3.
第二问中, 的取值为0,1,2,3. P(
的取值为0,1,2,3. P( =0)=
=0)= 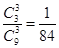 , P(
, P( =1)=
=1)= 
P( =2)=
=2)=  , P(
, P( =3)=
=3)= 
得到分布列和期望值
解:(I)据题意得到 解得m=6,n=3.
解得m=6,n=3.
(II) 的取值为0,1,2,3.
的取值为0,1,2,3.
P( =0)=
=0)= 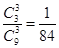 , P(
, P( =1)=
=1)= 
P( =2)=
=2)=  , P(
, P( =3)=
=3)= 
 的分布列为
的分布列为

所以E =2
=2
学校要用三辆车从北湖校区把教师接到文庙校区,已知从北湖校区到文庙校区有两条公路,汽车走公路①堵车的概率为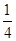 ,不堵车的概率为
,不堵车的概率为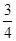 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为 ,不堵车的概率为
,不堵车的概率为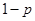 ,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为
,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为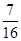 ,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数
,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数 的分布列和数学期望。
的分布列和数学期望。
【解析】第一问中,由已知条件结合n此独立重复试验的概率公式可知,得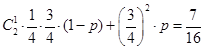
第二问中 可能的取值为0,1,2,3
可能的取值为0,1,2,3 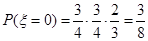 ,
, 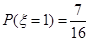
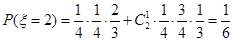 ,
,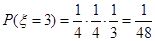
从而得到分布列和期望值
解:(I)由已知条件得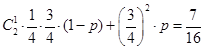 ,即
,即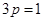 ,则
,则 的值为
的值为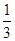 。
。
(Ⅱ) 可能的取值为0,1,2,3
可能的取值为0,1,2,3 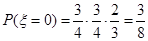 ,
, 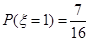
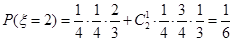 ,
,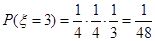
 的分布列为:(1分)
的分布列为:(1分)
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
所以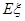
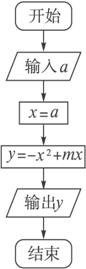
(1)图框中x=a的含义是什么?
(2)图框中y=-x2+mx的含义是什么?
(3)该程序框图解决的是怎样的一个?问题?
(4)当输入的x值为0和4时,输出的值相等,问当输入的x值为3时,输出的值为多大?
(5)要想使输出的值最大,输入的x值应为多少?
(6)按照这个程序框图,当输入的x的值都大于2时,x值大的输出的y值反而小,为什么?
若不等式 有唯一解,则
有唯一解,则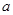 的取值为( )
的取值为( )
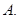 0
0 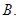 2
2
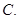 4
4
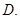 6
6
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com