
题目列表(包括答案和解析)
设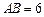 ,在线段
,在线段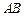 上任取两点C,D(端点
上任取两点C,D(端点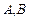 除外),将线段
除外),将线段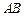 分成三条线段AC,CD,DB.
分成三条线段AC,CD,DB.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数摸拟的方法,来近似计算(Ⅱ)中事件B的概率.
20组随机数如下:
| | 1组 | 2组 | 3组 | 4组 | 5组 | 6组 | 7组 | 8组 | 9组 | 10组 |
| X | 0.52 | 0.36 | 0.58 | 0.73 | 0.41 | 0. 6 6 | 0.05 | 0.32 | 0.38 | 0.73 |
| Y | 0.76 | 0.39 | 0.37 | 0.01 | 0.04 | 0.28 | 0.03 | 0.15 | 0.14 | 0 .86 .86 |
| | 11组 | 12组 | 13组 | 14组 | 15组 | 16组 | 17组 | 18组 | 19组 | 20组 |
| X | 0.67 | 0.47 | 0.58 | 0.21 | 0.54 | 0. 64 64 | 0.36 | 0.35 | 0.95 | 0.14 |
| Y | 0.41 | 0.54 | 0.51 | 0.37 | 0.31 | 0.23 | 0.56 | 0.89 | 0.17 | 0.03 |
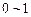 之间的均匀随机数,Y也是
之间的均匀随机数,Y也是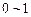 之间的均匀随机
之间的均匀随机 数)
数)(8分)
出租车司机从饭店到火车站途中有六个交通岗,假设他在各交通岗到红灯这一事件是相互独立的,并且概率都是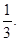
(I)求这位司机遇到红灯前,已经通过了两个交通岗的概率;
(II)求这位司机在途中遇到红灯数ξ的期望和方差。
设 ,
, ,
其中
,
其中 是不等于零的常数,
是不等于零的常数,
(1)、(理)写出 的定义域(2分);
的定义域(2分);
(文) 时,直接写出
时,直接写出 的值域(4分)
的值域(4分)
(2)、(文、理)求 的单调递增区间(理5分,文8分);
的单调递增区间(理5分,文8分);
(3)、已知函数
 ,定义:
,定义:
 ,
,
 .其中,
.其中, 表示函数
表示函数 在
在 上的最小值,
上的最小值,
 表示函数
表示函数 在
在 上的最大值.例如:
上的最大值.例如: ,
,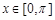 ,则
,则 ,
, ,
,
(理)当 时,设
时,设 ,不等式
,不等式
恒成立,求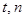 的取值范围(11分);
的取值范围(11分);
(文)当 时,
时, 恒成立,求
恒成立,求 的取值范围(8分);
的取值范围(8分);
(8分)如图,四棱锥 底面是正方形且四个顶点
底面是正方形且四个顶点 在球
在球 的同一个大圆(球面被过球心的平面截得的圆叫做大圆)上,点
的同一个大圆(球面被过球心的平面截得的圆叫做大圆)上,点 在球面上且
在球面上且 面
面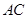 ,且已知
,且已知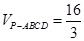 。
。
(1)求球 的体积;
的体积;
(2)设 为
为 中点,求异面直线
中点,求异面直线 与
与 所成角的余弦值。
所成角的余弦值。

设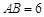 ,在线段
,在线段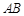 上任取两点C,D(端点
上任取两点C,D(端点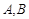 除外),将线段
除外),将线段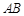 分成三条线段AC,CD,DB.
分成三条线段AC,CD,DB.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数摸拟的方法,来近似计算(Ⅱ)中事件B的概率.
20组随机数如下:
|
|
1组 |
2组 |
3组 |
4组 |
5组 |
6组 |
7组 |
8组 |
9组 |
10组 |
|
X |
0.52 |
0.36 |
0.58 |
0.73 |
0.41 |
0. 6 |
0.05 |
0.32 |
0.38 |
0.73 |
|
Y |
0.76 |
0.39 |
0.37 |
0.01 |
0.04 |
0.28 |
0.03 |
0.15 |
0.14 |
0.86 |
|
|
11组 |
12组 |
13组 |
14组 |
15组 |
16组 |
17组 |
18组 |
19组 |
20组 |
|
X |
0.67 |
0.47 |
0.58 |
0.21 |
0.54 |
0. 64 |
0.36 |
0.35 |
0.95 |
0.14 |
|
Y |
0.41 |
0.54 |
0.51 |
0.37 |
0.31 |
0.23 |
0.56 |
0.89 |
0.17 |
0.03 |
(X是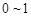 之间的均匀随机数,Y也是
之间的均匀随机数,Y也是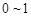 之间的均匀随机数)
之间的均匀随机数)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com