
题目列表(包括答案和解析)
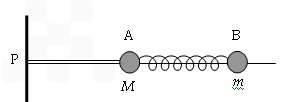
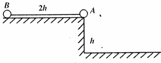 如图所示,质量均为m的小球A、B(可视为质点)用长为2h的细线相连,放在高为h的光滑水平桌面上,A球刚好在桌边,现使小球A由静止开始下落,若A、B两球落地后均不再弹起,则下面说法正确的是( )
如图所示,质量均为m的小球A、B(可视为质点)用长为2h的细线相连,放在高为h的光滑水平桌面上,A球刚好在桌边,现使小球A由静止开始下落,若A、B两球落地后均不再弹起,则下面说法正确的是( )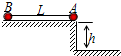 如图所示,质量均为m的小球A、B用长为L的细线相连,放在高为h的光滑水平桌面上(L>2h),A球刚好在桌边.从静止释放两球,若A、B两球落地后均不再弹起,则下面说法中不正确的是( )
如图所示,质量均为m的小球A、B用长为L的细线相连,放在高为h的光滑水平桌面上(L>2h),A球刚好在桌边.从静止释放两球,若A、B两球落地后均不再弹起,则下面说法中不正确的是( )(18分)如图所示,质量均为m的两球AB间有压缩的轻、短弹簧处于锁定状态,放置在水平面上竖直光滑的发射管内(两球的大小尺寸和弹簧尺寸都可忽略,他们整体视为质点),解除锁定时,A球能上升的最大高度为H,现在让两球包括锁定的弹簧从水平面出发,沿光滑的半径为R的半圆槽从右侧由静止开始下滑,至最低点时,瞬间锁定解除,求A球离开圆槽后能上升的最大高度。
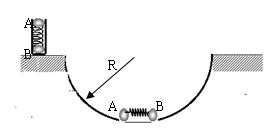
如图所示,质量均为m的小球A、B用两根不可伸长的轻绳连接后悬挂于D点,在外力F的作用下,小球A、B处于静止状态,若要使两小球处于静止状态且悬线OA与竖直方向的夹角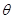 保持30°不变,则外力F的大小不可能是
保持30°不变,则外力F的大小不可能是
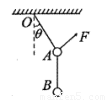
A.可能为mg
B.可能为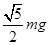
C.可能为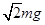
D.可能为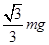
一.选择题:(每小题4分,选不全者得2分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
D
D
AC
AD
C
ACD
AD
ABC
二.实验题:(每空2分共12分)
11.①0.75 ②1.25
12. ⑴
三.计算题:
13.(10分)解:-μmg=ma,解得:a=-μg 2分
因此:.files/image055.gif) 2分
2分
由运动学公式:.files/image057.gif) 2分
2分
得:.files/image059.gif) ,即:
,即:.files/image061.gif) 4分
4分
14.(10分)解(1)月球表面的重力加速度为g,h=.files/image063.gif) gt2 ①
gt2 ①
得.files/image065.gif) ……………………………………………………2分
……………………………………………………2分
(2)设月球的质量为M,月球半径为r,由万有引力定律和向心力公式得:
.files/image067.gif) =mg ②……………………………………3分
=mg ②……………………………………3分
.files/image067.gif) =
=.files/image069.gif) ③……………………………………3分
③……………………………………3分
联立①②③式可得:.files/image071.gif) ………………………2分
………………………2分
15.(14分)解:解除锁定后弹簧将弹性势能全部转化为A的机械能
,则弹簧弹性势能为 E弹=mgH ①………………2分
AB系统由水平位置滑到圆轨道最低点时速度为v0 , 解除弹簧锁定后A、B的速度分别为vA、vB 则有
2mgR=2×.files/image073.gif) ②………………2分
②………………2分
2×.files/image073.gif) + E弹= m vA2/2+
m vB2/2
④……………2分
+ E弹= m vA2/2+
m vB2/2
④……………2分
将 vB=2 v0 -vA代入能量关系得到
2mgR+mgH= m vA2/2+
m (2 v0 -vA)2/2 v0 =.files/image076.gif) ⑤…………2分
⑤…………2分
得到: vA =.files/image076.gif) +
+.files/image079.gif) ⑥…………2分
⑥…………2分
相对水平面上升最大高度h, 则: mg(h+R)= .files/image081.gif) ⑦…………1分
⑦…………1分
h=H/2+.files/image083.gif) ⑧…………1分
⑧…………1分
16.(14分)解析:(1)木块A和滑板B均向左做匀加速直线运动
.files/image085.gif)
根据题意有:.files/image087.gif) 即
即.files/image089.gif) 代入数据得:t=1s……3分
代入数据得:t=1s……3分
(2)1秒末木块A和滑板B的速度分别为:
.files/image091.gif) ,
,.files/image093.gif)
当木块A和滑板B的速度相同时,弹簧压缩量最大,具有最大弹性势能。
根据动量守恒定律有
.files/image095.gif) ……………………2分
……………………2分
由能量守恒定律得
.files/image097.gif) ………2分
………2分
代入数据求得.files/image099.gif) ……………………………………………………….1分
……………………………………………………….1分
(3)假设木块相对木板向左运动离开弹簧后系统又能达到共同速度v’,相对木板向左滑动距离s,有 .files/image095.gif) ’……………………………………2分
’……………………………………2分
.files/image101.gif) ………………………………2分
………………………………2分
得s=
由于x+L>s且s>x,故假设成立,
整个过程系统产生的热量为.files/image103.gif) =1.4J………………………2分
=1.4J………………………2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com