
题目列表(包括答案和解析)
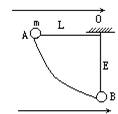 在电场强度为E=104N/C、方向水平向右的匀强电场中,用一根长l=1m的绝缘细杆(质量不计)固定一个质量为m=0.02kg的电量为q=5×10-6C带正电的小球,细杆可绕轴O在竖直平面内自由转动。现将杆从水平位置A轻轻释放,在小球运动到最低点B的过程中,电场力对小球作功多少?A、B两位置的电势差多少?小球的电势能如何变化?小球到达B点时的速度多大?取g=10m/s2
在电场强度为E=104N/C、方向水平向右的匀强电场中,用一根长l=1m的绝缘细杆(质量不计)固定一个质量为m=0.02kg的电量为q=5×10-6C带正电的小球,细杆可绕轴O在竖直平面内自由转动。现将杆从水平位置A轻轻释放,在小球运动到最低点B的过程中,电场力对小球作功多少?A、B两位置的电势差多少?小球的电势能如何变化?小球到达B点时的速度多大?取g=10m/s2
 有一带负电的小球,其带电量q=-2×10-3C.如图所示,开始时静止在场强E=200N/C的匀强电场中的P点,靠近电场极板B有一挡板要S,小球与挡板S的距离h=5cm,与A板距离H=45cm,重力作用不计.在电场力作用下小球向左运动,与挡板S相碰后电量减少到碰前的k倍,已知k=
有一带负电的小球,其带电量q=-2×10-3C.如图所示,开始时静止在场强E=200N/C的匀强电场中的P点,靠近电场极板B有一挡板要S,小球与挡板S的距离h=5cm,与A板距离H=45cm,重力作用不计.在电场力作用下小球向左运动,与挡板S相碰后电量减少到碰前的k倍,已知k=| 5 | 6 |
| 5 |
| 6 |
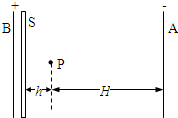
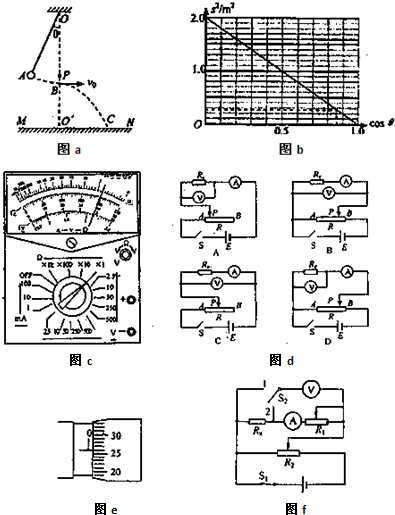
竖直平面内,一带正电的小球,系于长为L的不可伸长的轻线一端,线的另一端固定为O点,它们处在匀强电场中,电场的方向水平向右,场强的大小为E. 已知电场对小球的作用力的大小等于小球的重力. 现先把小球拉到图中的P1处,使轻线伸直,并与场强方向平行,然后由静止释放小球.已知小球在经过最低点的瞬间,因受线的拉力作用,其速度的竖直速度突变为零,水平分量没有变化,(不计空气阻力)则小球到达与P1点等高的P2时线上张力T为多少( )

A.mg B.3mg
C.4mg D.5mg
一、选择题
题 号
1
2
3
4
5
6
答 案
CD
BD
AD
C
ABCD
C
题 号
7
8
9
10
11
12
答 案
C
ABC
C
C
D
D
二、实验题
13、(1)甲 (2)1.14 、13.873或13.874
14、(1)ABC (2)⑦用同一标度作出这个力F′的图示.(注:没有“同一标度”不给分);⑨误差允许范围内F′与F大小相等,方向相同.(注:没有“在误差允许范围内扣一分)
15、0.86、0.64
三、计算题
16、解:(1)(M+m)g (3分)
(2)mgctgα (3分)
17、解:(1)对小物受力分析,由牛顿运动??定律得:
??????高三年级第一次摸底考试(物理).files/image036.gif) ?(2分)
?(2分)
??????高三年级第一次摸底考试(物理).files/image038.gif) (2分)
(2分)
??????解得:v= 高三年级第一次摸底考试(物理).files/image040.gif) m/s(1分)
m/s(1分)
????(2)高三年级第一次摸底考试(物理).files/image042.gif) ??(1分)
??(1分)
??????高三年级第一次摸底考试(物理).files/image044.gif) ?(1分)
?(1分)
??????解得:x=高三年级第一次摸底考试(物理).files/image046.gif) m(1分)
m(1分)
18、解:(1)设A在C板上滑动时,B相对于C板不动,则对B、C有?
μmg=2ma (1分)
高三年级第一次摸底考试(物理).files/image048.gif) ?(1分)
?(1分)
又B依靠摩擦力能获得的最大加速度为 am=高三年级第一次摸底考试(物理).files/image050.gif) =
=高三年级第一次摸底考试(物理).files/image052.gif) (1分)
(1分)
∵am>a?∴ B未相对C滑动而随木板C向右做加速运动 ?(1分)
B受到的摩擦力fb = ma
=高三年级第一次摸底考试(物理).files/image054.gif) μmg (1分)
μmg (1分)
(2)要使物块A刚好与物块B发生碰撞,物块A运动到物块B处时,A、B的速度相等,即v1=
v0-μgt =高三年级第一次摸底考试(物理).files/image054.gif) μgt (2分) 得v1=
v0/3 (1分)
μgt (2分) 得v1=
v0/3 (1分)
设木板C在此过程中的位移为x1,则物块A的位移为x1+x,由动能定理?
-μmg(x1+x)
= 高三年级第一次摸底考试(物理).files/image054.gif) mv12-
mv12-高三年级第一次摸底考试(物理).files/image054.gif) mv02 (1分)
mv02 (1分)
μmgx1 =高三年级第一次摸底考试(物理).files/image054.gif) (2m)v12 (1分)
(2m)v12 (1分)
联立上述各式解得v0
=高三年级第一次摸底考试(物理).files/image056.gif)
要使物块A、B发生相碰的条件是v0>高三年级第一次摸底考试(物理).files/image056.gif) (1分)
(1分)
| ||||||||||||||||||||||||||||||||||||