练习册

  • 练习册
  • 试题
    已知函数.这里, 【查看更多】

     

    题目列表(包括答案和解析)

    已知函数f（x）=ln（1+x）-ax．
    （1）讨论函数f（x）在定义域内的最值（4分）；
    （2）已知数列{an}满足a1=1，an+1=(1+
    1
    n2
    )an+
    1
    2n
    (n∈N+)    ．
    ①证明对一切n∈N+且n≥2，an≥2（4分）；
    ②证明对一切n∈N+，an＜e3（这里e是自然对数的底数）（6分）．

    查看答案和解析>>

    已知函数f（x）是奇函数，f（x）的定义域为（-∞，+∞）．当x＜0时，f（x）=
    ln(-ex)
    x
    ．这里，e为自然对数的底数．
    （1）若函数f（x）在区间(a，a+
    1
    3
    )(a＞0)    上存在极值点，求实数a的取值范围；
    （2）如果当x≥1时，不等式f(x)≥
    k
    x+1
    恒成立，求实数k的取值范围；
    （3）试判断 ln
    1
    n+1
    与2(
    1
    2
    +
    2
    3
    +…+
    n
    n+1
    )-n    的大小关系，这里n∈N*，并加以证明．

    查看答案和解析>>

    已知函数。

    （1）讨论函数在定义域内的最值（4分）；

    （2）已知数列满足。

    ① 证明对一切且，（4分）；

    ② 证明对一切，（这里是自然对数的底数）（6分）。

     

    查看答案和解析>>

    已知函数f（x）=ln（1+x）-ax．
    （1）讨论函数f（x）在定义域内的最值（4分）；
    （2）已知数列{an}满足数学公式．
    ①证明对一切n∈N+且n≥2，an≥2（4分）；
    ②证明对一切n∈N+，an＜e3（这里e是自然对数的底数）（6分）．

    查看答案和解析>>

    已知函数数学公式．
    （Ⅰ）求函数f（x）的单调区间和极值；
    （Ⅱ）若（et+2）x2+etx+et-2≥0对满足|x|≤1的任意实数x恒成立，求实数t的取值范围（这里e是自然对数的底数）；
    （Ⅲ）求证：对任意正数a、b、λ、μ，恒有数学公式数学公式．

    查看答案和解析>>

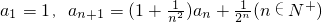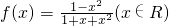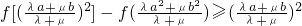
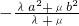    一、选择题：

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    答案

    C

    D

    D

    A

    B

    D

    B

    C

    B

    C

    D

    B

    1．提示：所以，故选C。

    2．提示：命题P：，所以命题P是假命题，

    命题Q

    当时，。 ，所以以命题Q是真命题，故选D。故选A。

    3．提示：又，所以，故选D。

    4．提示：在AB上取点D，使得，则点P只能在AD内运动，则，

    5．提示：故选B。

    6．提示：由图（1）改为图（2）后每次循环时的值都为1，因此运行过程出现无限循环，故选D

    7．提示：设全班40个人的总分为S，

    则，故选B。

    8．提示：

    所以约束条件为表示的平面区域是以点O（0，0），，N（0，1），Q（2，3）为顶点的平行四边形（包括边界），故当时，的最大值是4，故选C。

    9．提示：由及得

    如图

    过A作于M,则

     得.

    故选B.

    10．提示：不妨设点（2，0）与曲线上不同的三的点距离为分别，它们组成的等比数列的公比为若令，显然，又所以，不能取到。故选B。

    11．提示：使用特值法：取集合当可以排除A、B；

    取集合，当可以排除C；故选D；

    12．提示：n棱柱有个顶点，被平面截去一个三棱锥后，可以分以下6种情形（图1~6）

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

    在图4，图6所示的情形，还剩个顶点；

    在图5的情形，还剩个顶点；

    在图2，图3的情形，还剩个顶点；

    在图1的情形，还剩下个顶点.故选B.

    二、填空题：

    13．   

    提示：由

    14． 

    提示：斜率 ，切点，所以切线方程为：

    15．

    提示：当时，不等式无解，当时，不等式变为 ，

    由题意得或，所以，或

    16．

    三、解答题：

    17．解：① ∵∴的定义域为R；

    ② ∵，

     ∴为偶函数；

    ③ ∵,  ∴是周期为的周期函数；

    ④ 当时，= ，

    ∴当时单调递减；当时，

    =，

    单调递增；又∵是周期为的偶函数，∴在上单调递增，在上单调递减（）；

    ⑤ ∵当时；

    当时．∴的值域为；

     ⑥由以上性质可得：在上的图象如图所示：

     

     

     

     

    18．解：（Ⅰ）取PC的中点G，连结EG，GD，则

    由（Ⅰ）知FD⊥平面PDC，面PDC，所以FD⊥DG。

    所以四边形FEGD为矩形，因为G为等腰Rt△RPD斜边PC的中点，

    所以DG⊥PC，

    所以DG⊥平面PBC.

    因为DG//EF，所以EF⊥平面PBC。

    （Ⅱ） 

     

     

     

     

    19．解：（1）；根据题意：为的二个根；

         由于；； 

         所以；

          （2）由为的二个根；所以；

    所以：

           ；

         又

    所以：；故：线段的中点在曲线上；

    20．解：

    分别记“客人浏览甲、乙、丙景点”为事件。则相互独立，且

    客人浏览景点数可能取值为0、1、2、3；相应在客人没有浏览的景点数的可能取值为3、2、1、0

    而

    的分布列为

    1

    3

    p

    0．76

    0．24

    则

    （2）

    在上单调递增，那么要在上单调递增，必须，即

    故

     

    21．解：（1）由已知，当时，

    又，

    当时，，

    两式相减得：

    当时，适合上式，

    （2）由（1）知

    当时，

    两式相减得：

    ，则数列是等差数列，首项为1，公差为1。

    （3）

    要使得恒成立，

    恒成立，

    即恒成立。

    当为奇数时，即恒成立，又的最小值为1，

    当为偶数时，即恒成立，又的最大值为，

    即又为整数，

    ，使得对任意，都有

    22．解：（1）由题意知则

    解得而，故，

    所以函数在区间 上单调递增。

    （2）由得

    所以点G的坐标为

    函数在区间 上单调递增。

    所以当时，取得最小值，此时点F、G的坐标分别为

    由题意设椭圆方程为，由于点G在椭圆上，得

    解得

    所以得所求的椭圆方程为。

    （3）设C，D的坐标分别为，则

    由，得，

    因为，点C、D在椭圆上，，，

    消去得。又，解得

    所以实数的取值范围是

     

     

     

     

     

     

     

     

     


    同步练习册答案