
题目列表(包括答案和解析)
求由抛物线 与直线
与直线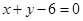 及
及 所围成图形的面积.
所围成图形的面积.
【解析】首先利用已知函数和抛物线作图,然后确定交点坐标,然后利用定积分表示出面积为 ,所以得到
,所以得到 ,由此得到结论为
,由此得到结论为
解:设所求图形面积为 ,则
,则

 =
= .即所求图形面积为
.即所求图形面积为 .
.

已知p:,q:,若p是![]() q的充分不必要条件则实数m的取值范围
q的充分不必要条件则实数m的取值范围
(天津卷理9)已知函数![]() 是R上的偶函数,且在区间
是R上的偶函数,且在区间![]() 上是增函数.令
上是增函数.令![]() ,则
,则
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(本题9分)已知函数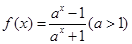 .
.
(1) 判断函数的奇偶性; (2) 求该函数的值域;⑶ 利用定义法证明 是
是 上的增函数
上的增函数
(A)偶函数且它的图象关于点(π,0)对称
(B)偶函数且它的图象关于点(![]() ,0)对称
,0)对称
(C)奇函数且它的图象关于点(![]() ,0)对称
,0)对称
(D)奇函数且它的图象关于点(π,0)对称
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com