
题目列表(包括答案和解析)
为了了解某市工人开展体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,计算这2个工厂中至少有1个来自A区的概率.
【解析】本试题主要考查了统计和概率的综合运用。
第一问工厂总数为18+27+18=63,样本容量与总体中的个体数比为7/63=1/9…3分
所以从A,B,C三个区中应分别抽取的工厂个数为2,3,2。
第二问设A1,A2为在A区中的抽得的2个工厂,B1,B2,B3为在B区中抽得的3个工厂,
C1,C2为在C区中抽得的2个工厂。
这7个工厂中随机的抽取2个,全部的可能结果有1/2*7*6=32种。
随机的抽取的2个工厂至少有一个来自A区的结果有A1,A2),A1,B2),A1,B1),
A1,B3)A1,C2),A1,C1), …………9分
同理A2还能给合5种,一共有11种。
所以所求的概率为p=11/21
2010年11月广州成功举办了第十六届亚运会。在华南理工大学学生会举行的亚运知识有奖问答比赛中,甲、乙、丙同时回答一道有关亚运知识的问题,已知甲回答对这道题目的概率是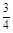 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是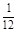 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是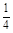 .
.
(1)求乙、丙两人各自回答对这道题目的概率.
(2)(理)求回答对这道题目的人数的随机变量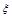 的分布列和期望.
的分布列和期望.
【解析】本试题主要考查了独立事件概率的乘法计算公式的运用。以及对立事件的概率的运用。
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数。
(1)sin213°+cos217°-sin13°cos17°
(2)sin215°+cos215°-sin15°cos15°
(3)sin218°+cos212°-sin18°cos12°
(4)sin2(-18°)+cos248°- sin2(-18°)cos248°
(5)sin2(-25°)+cos255°- sin2(-25°)cos255°
Ⅰ 试从上述五个式子中选择一个,求出这个常数
Ⅱ 根据(Ⅰ)的计算结果,将该同学的发现推广位三角恒等式,并证明你的结论
【解析】
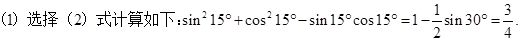
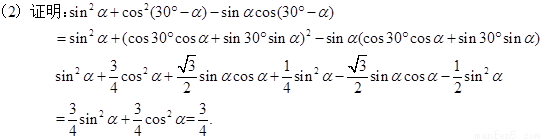
零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识,考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分
【解析】(Ⅰ)解:由所给数据可知,一等品零件共有6个.设“从10个零件中,随机抽取一个为一等品”为事件A,则P(A)=![]() =
=![]() .
.
(Ⅱ)(i)解:一等品零件的编号为![]() .从这6个一等品零件中随机抽取2个,所有可能的结果有:
.从这6个一等品零件中随机抽取2个,所有可能的结果有:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 共有15种.
共有15种.
(ii)解:“从一等品零件中,随机抽取的2个零件直径相等”(记为事件B)的所有可能结果有:![]() ,
,![]() ,共有6种.
,共有6种.
所以P(B)=![]() .
.
(本小题满分12分)
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=![]() ,∠BAD=∠CDA=45°.
,∠BAD=∠CDA=45°.
 (Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅱ)证明CD⊥平面ABF;
(Ⅲ)求二面角B-EF-A的正切值。
已知函数 , 其中
, 其中 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,求曲线
时,求曲线 的单调区间与极值.
的单调区间与极值.
【解析】第一问中利用当 时,
时, ,
,
 ,得到切线方程
,得到切线方程
第二问中,

对a分情况讨论,确定单调性和极值问题。
解: (1) 当 时,
时, ,
,
 ………………………….2分
………………………….2分

 切线方程为:
切线方程为:  …………………………..5分
…………………………..5分
(2) 
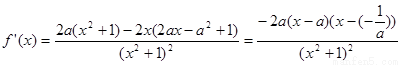 …….7
…….7 分
分
分类: 当 时, 很显然
时, 很显然
 的单调增区间为:
的单调增区间为:  单调减区间:
单调减区间:  ,
,
 ,
,  ………… 11分
………… 11分
当 时
时 的单调减区间:
的单调减区间:  单调增区间:
单调增区间: 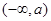 ,
,

 ,
, 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com