
题目列表(包括答案和解析)
(本小题满分12分) 已知点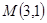 ,直线
,直线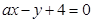 及圆
及圆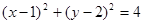 .
.
(1)求过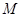 点的圆的切线方程;
点的圆的切线方程;
(2)若直线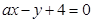 与圆相切,求
与圆相切,求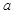 的值;
的值;
(3)若直线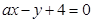 与圆相交于
与圆相交于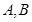 两点,且弦
两点,且弦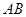 的长为
的长为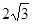 ,求
,求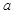 的值.
的值.
已知圆![]() ,直线
,直线![]() 过定点A(1,0).
过定点A(1,0).
(1)若![]() 与圆相切,求
与圆相切,求![]() 的方程;
的方程;
(2)若![]() 与圆相交于P,Q两点,线段PQ的中点为M,又
与圆相交于P,Q两点,线段PQ的中点为M,又![]() 与
与![]() 的交点为N,判断
的交点为N,判断![]() 是否为定值,若是,则求出定值;若不是,请说明理由.
是否为定值,若是,则求出定值;若不是,请说明理由.
已知圆C:(x-3)2+(y-4)2=4,直线![]() 过定点A(1,0)
过定点A(1,0)
(1)若直线![]() 与圆C相切,求直线
与圆C相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆C相交于P,Q两点,线段PQ中点为M,又直线
与圆C相交于P,Q两点,线段PQ中点为M,又直线![]() 与直线x+2y+2=0的交点为N,判断AM?AN是否为定值?若是,则求出定值;若不是,说明理由。
与直线x+2y+2=0的交点为N,判断AM?AN是否为定值?若是,则求出定值;若不是,说明理由。
若直线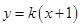 与圆
与圆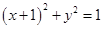 相交于
相交于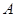 、
、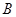 两点,则
两点,则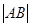 的值为( )
的值为( )
A.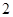 B.
B.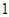 C.
C. D.与
D.与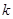 有关的数值
有关的数值
已知倾斜角为![]() 的直线
的直线![]() 过点
过点![]() 和点
和点![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 。(1)求点
。(1)求点![]() 的坐标;高考资源网(2)若直线
的坐标;高考资源网(2)若直线![]() 与双曲线
与双曲线![]() 相交于
相交于![]() 两点,且线段
两点,且线段![]() 的中点坐标为
的中点坐标为![]() ,求
,求![]() 的值;高考资源网3)对于平面上任一点
的值;高考资源网3)对于平面上任一点![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,称
上运动时,称![]() 的最小值为
的最小值为![]() 与线段
与线段![]() 的距离。已知
的距离。已知![]() 在
在![]() 轴上运动,写出点
轴上运动,写出点![]() 到线段
到线段![]() 的距离
的距离![]() 关于
关于![]() 的函数关系式。
的函数关系式。
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 第Ⅰ部分(正卷)
第Ⅰ部分(正卷)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 一、填空题:本大题共14小题,每小题5分,计70分。
一、填空题:本大题共14小题,每小题5分,计70分。
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 1、
1、/江苏省镇江市2009届高三第三次调研测试(数学).files/image213.gif) 2、
2、/江苏省镇江市2009届高三第三次调研测试(数学).files/image215.gif) 3、对任意
3、对任意/江苏省镇江市2009届高三第三次调研测试(数学).files/image014.gif) 使
使/江苏省镇江市2009届高三第三次调研测试(数学).files/image218.gif) 4、2 5、
4、2 5、/江苏省镇江市2009届高三第三次调研测试(数学).files/image220.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 6、
6、/江苏省镇江市2009届高三第三次调研测试(数学).files/image222.gif) 7、
7、/江苏省镇江市2009届高三第三次调研测试(数学).files/image224.gif) 8、8
9、
8、8
9、/江苏省镇江市2009届高三第三次调研测试(数学).files/image226.gif) 10、40
10、40
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 11、
11、/江苏省镇江市2009届高三第三次调研测试(数学).files/image228.gif) 12、4
13、
12、4
13、/江苏省镇江市2009届高三第三次调研测试(数学).files/image230.gif) 14、
14、/江苏省镇江市2009届高三第三次调研测试(数学).files/image232.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image234.jpg)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 二、解答题:本大题共6小题,计90分。解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内。
二、解答题:本大题共6小题,计90分。解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内。
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 15、解:(1)解:
15、解:(1)解:/江苏省镇江市2009届高三第三次调研测试(数学).files/image236.gif) ,
,
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 由
由/江苏省镇江市2009届高三第三次调研测试(数学).files/image116.gif) ,有
,有/江苏省镇江市2009届高三第三次调研测试(数学).files/image239.gif) ,
,
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 解得
解得/江苏省镇江市2009届高三第三次调研测试(数学).files/image241.gif) 。
……7分
。
……7分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) (2)解法一:
(2)解法一:/江苏省镇江市2009届高三第三次调研测试(数学).files/image243.gif) ……11分
……11分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image245.gif) 。 ……14分
。 ……14分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 解法二:由(1),
解法二:由(1),/江苏省镇江市2009届高三第三次调研测试(数学).files/image241.gif) ,得
,得/江苏省镇江市2009届高三第三次调研测试(数学).files/image248.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image250.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image252.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image254.gif) ……10分
……10分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 于是
于是/江苏省镇江市2009届高三第三次调研测试(数学).files/image256.gif) ,
,
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image258.gif) ……12分
……12分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 代入得
代入得/江苏省镇江市2009届高三第三次调研测试(数学).files/image260.gif) 。
……14分
。
……14分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 16、证明:(1)∵
16、证明:(1)∵/江苏省镇江市2009届高三第三次调研测试(数学).files/image130.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image263.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image132.gif) ……4分
……4分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) (2)令
(2)令/江苏省镇江市2009届高三第三次调研测试(数学).files/image266.gif) 中点为
中点为/江苏省镇江市2009届高三第三次调研测试(数学).files/image168.gif) ,
,/江苏省镇江市2009届高三第三次调研测试(数学).files/image269.gif) 中点为
中点为/江苏省镇江市2009届高三第三次调研测试(数学).files/image271.gif) ,连结
,连结/江苏省镇江市2009届高三第三次调研测试(数学).files/image148.gif) 、
、/江苏省镇江市2009届高三第三次调研测试(数学).files/image274.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∵
∵/江苏省镇江市2009届高三第三次调研测试(数学).files/image148.gif) 是
是/江苏省镇江市2009届高三第三次调研测试(数学).files/image277.gif) 的中位线
的中位线
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image279.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image281.gif) ……6分
……6分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 又∵
又∵/江苏省镇江市2009届高三第三次调研测试(数学).files/image130.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image284.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image286.gif) ……8分
……8分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image288.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∵
∵/江苏省镇江市2009届高三第三次调研测试(数学).files/image097.gif) 为正
为正/江苏省镇江市2009届高三第三次调研测试(数学).files/image291.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image293.gif) ……10分
……10分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image295.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 又∵
又∵/江苏省镇江市2009届高三第三次调研测试(数学).files/image297.gif) ,
,/江苏省镇江市2009届高三第三次调研测试(数学).files/image284.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴四边形
∴四边形/江苏省镇江市2009届高三第三次调研测试(数学).files/image300.gif) 为平行四边形 ……12分
为平行四边形 ……12分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image302.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image136.gif) ……14分
……14分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image234.jpg)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 17、解:(1)设
17、解:(1)设/江苏省镇江市2009届高三第三次调研测试(数学).files/image305.gif) 米,
米,/江苏省镇江市2009届高三第三次调研测试(数学).files/image307.gif) ,则
,则/江苏省镇江市2009届高三第三次调研测试(数学).files/image309.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∵
∵/江苏省镇江市2009届高三第三次调研测试(数学).files/image311.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image313.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image315.gif) ……2分
……2分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image317.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image319.gif) ……4分
……4分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image321.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image323.gif) 或
或/江苏省镇江市2009届高三第三次调研测试(数学).files/image325.gif) ……5分
……5分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) (2)
(2)/江苏省镇江市2009届高三第三次调研测试(数学).files/image327.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image329.gif) ……7分
……7分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image331.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image333.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 此时
此时/江苏省镇江市2009届高三第三次调研测试(数学).files/image335.gif) ……10分
……10分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) (3)∵
(3)∵/江苏省镇江市2009届高三第三次调研测试(数学).files/image337.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image339.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 令
令/江苏省镇江市2009届高三第三次调研测试(数学).files/image341.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image343.gif) ,
,/江苏省镇江市2009届高三第三次调研测试(数学).files/image345.gif) ……11分
……11分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∵
∵/江苏省镇江市2009届高三第三次调研测试(数学).files/image347.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 当
当/江苏省镇江市2009届高三第三次调研测试(数学).files/image349.gif) 时,
时,/江苏省镇江市2009届高三第三次调研测试(数学).files/image351.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image345.gif) 在
在/江苏省镇江市2009届高三第三次调研测试(数学).files/image354.gif) 上递增
……13分
上递增
……13分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image356.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 此时
此时/江苏省镇江市2009届高三第三次调研测试(数学).files/image358.gif) ……14分
……14分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 答:(1)
答:(1)/江苏省镇江市2009届高三第三次调研测试(数学).files/image360.gif) 或
或/江苏省镇江市2009届高三第三次调研测试(数学).files/image362.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) (2)当
(2)当/江苏省镇江市2009届高三第三次调研测试(数学).files/image146.gif) 的长度是
的长度是/江苏省镇江市2009届高三第三次调研测试(数学).files/image142.gif) 的面积最小,最小面积为24平方米;
的面积最小,最小面积为24平方米;
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) (3)当
(3)当/江苏省镇江市2009届高三第三次调研测试(数学).files/image146.gif) 的长度是
的长度是/江苏省镇江市2009届高三第三次调研测试(数学).files/image142.gif) 的面积最小,
的面积最小,
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 最小面积为27平方米。 ……15分
最小面积为27平方米。 ……15分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 18、(1)解:①若直线
18、(1)解:①若直线/江苏省镇江市2009届高三第三次调研测试(数学).files/image156.gif) 的斜率不存在,即直线是
的斜率不存在,即直线是/江苏省镇江市2009届高三第三次调研测试(数学).files/image369.gif) ,符合题意。 ……2分
,符合题意。 ……2分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image371.jpg)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ②若直线
②若直线/江苏省镇江市2009届高三第三次调研测试(数学).files/image156.gif) 斜率存在,设直线
斜率存在,设直线/江苏省镇江市2009届高三第三次调研测试(数学).files/image156.gif) 为
为/江苏省镇江市2009届高三第三次调研测试(数学).files/image375.gif) ,即
,即/江苏省镇江市2009届高三第三次调研测试(数学).files/image377.gif) 。
。
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 由题意知,圆心
由题意知,圆心/江苏省镇江市2009届高三第三次调研测试(数学).files/image379.gif) 以已知直线
以已知直线/江苏省镇江市2009届高三第三次调研测试(数学).files/image156.gif) 的距离等于半径2,即:
的距离等于半径2,即:/江苏省镇江市2009届高三第三次调研测试(数学).files/image382.gif) ,
,
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 解之得
解之得/江苏省镇江市2009届高三第三次调研测试(数学).files/image384.gif) ……5分
……5分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 所求直线方程是
所求直线方程是/江苏省镇江市2009届高三第三次调研测试(数学).files/image369.gif) ,
,/江苏省镇江市2009届高三第三次调研测试(数学).files/image387.gif) ……6分
……6分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) (2)解法一:直线与圆相交,斜率必定存在,且不为0,可设直线方程为
(2)解法一:直线与圆相交,斜率必定存在,且不为0,可设直线方程为/江苏省镇江市2009届高三第三次调研测试(数学).files/image377.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 由
由/江苏省镇江市2009届高三第三次调研测试(数学).files/image390.gif) 得
得/江苏省镇江市2009届高三第三次调研测试(数学).files/image392.gif) ……8分
……8分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) 又直线
又直线/江苏省镇江市2009届高三第三次调研测试(数学).files/image394.gif) 与
与/江苏省镇江市2009届高三第三次调研测试(数学).files/image156.gif) 垂直,由
垂直,由/江苏省镇江市2009届高三第三次调研测试(数学).files/image397.gif) 得
得/江苏省镇江市2009届高三第三次调研测试(数学).files/image399.gif) ……11分
……11分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image401.gif)
/江苏省镇江市2009届高三第三次调研测试(数学).files/image138.jpg) ……13分
……13分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image403.gif) 为定值。
为定值。
故/江苏省镇江市2009届高三第三次调研测试(数学).files/image405.gif) 是定值,且为6。
……15分
是定值,且为6。
……15分
19、解:(1)由题意得/江苏省镇江市2009届高三第三次调研测试(数学).files/image407.gif) ,
……2分
,
……2分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image327.gif) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image409.gif) ,
,/江苏省镇江市2009届高三第三次调研测试(数学).files/image411.gif) ∴
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image413.gif) ……3分
……3分
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image415.gif) ,∴
,∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image417.gif) 在
在/江苏省镇江市2009届高三第三次调研测试(数学).files/image419.gif) 是
是
单调增函数, ……5分
∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image421.gif) 对于
对于/江苏省镇江市2009届高三第三次调研测试(数学).files/image423.gif) 恒成立。 ……6分
恒成立。 ……6分
(2)方程/江苏省镇江市2009届高三第三次调研测试(数学).files/image189.gif) ; ∴
; ∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image426.gif) ……7分
……7分
∵/江苏省镇江市2009届高三第三次调研测试(数学).files/image428.gif) ,∴方程为
,∴方程为/江苏省镇江市2009届高三第三次调研测试(数学).files/image430.gif) ……9分
……9分
令/江苏省镇江市2009届高三第三次调研测试(数学).files/image432.gif) ,
,/江苏省镇江市2009届高三第三次调研测试(数学).files/image434.gif) ,
,
∵/江苏省镇江市2009届高三第三次调研测试(数学).files/image436.gif) ,当
,当/江苏省镇江市2009届高三第三次调研测试(数学).files/image438.gif) 时,
时,/江苏省镇江市2009届高三第三次调研测试(数学).files/image440.gif) ,∴
,∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image442.gif) 在
在/江苏省镇江市2009届高三第三次调研测试(数学).files/image444.gif) 上为增函数;
上为增函数;
/江苏省镇江市2009届高三第三次调研测试(数学).files/image446.gif) 时,
时,/江苏省镇江市2009届高三第三次调研测试(数学).files/image448.gif) , ∴
, ∴/江苏省镇江市2009届高三第三次调研测试(数学).files/image442.gif) 在
在/江苏省镇江市2009届高三第三次调研测试(数学).files/image451.gif) 上为减函数, ……12分
上为减函数, ……12分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image453.jpg) 当
当/江苏省镇江市2009届高三第三次调研测试(数学).files/image455.gif) 时,
时,/江苏省镇江市2009届高三第三次调研测试(数学).files/image457.gif) ……13分
……13分
/江苏省镇江市2009届高三第三次调研测试(数学).files/image459.gif) ,
,
∴函数/江苏省镇江市2009届高三第三次调研测试(数学).files/image461.gif) 、
、/江苏省镇江市2009届高三第三次调研测试(数学).files/image463.gif) 在同一坐标系的大致图象如图所示,
在同一坐标系的大致图象如图所示,
∴①当/江苏省镇江市2009届高三第三次调研测试(数学).files/image465.gif) ,即
,即/江苏省镇江市2009届高三第三次调研测试(数学).files/image467.gif) 时,方程无解。
时,方程无解。
②当/江苏省镇江市2009届高三第三次调研测试(数学).files/image469.gif) ,即
,即/江苏省镇江市2009届高三第三次调研测试(数学).files/image471.gif) 时,方程有一个根。
时,方程有一个根。
③当/江苏省镇江市2009届高三第三次调研测试(数学).files/image473.gif) ,即
,即/江苏省镇江市2009届高三第三次调研测试(数学).files/image475.gif) 时,方程有两个根。 ……16分
时,方程有两个根。 ……16分
第Ⅱ部分(附加卷)
一、必做题
21、解:(1)由/江苏省镇江市2009届高三 </div>
</div>
<div class=)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com