查看答案和解析>>

某研究机构为了研究人的脚的大小与身高之间的关系，随机抽测了20人，得到如下数据:

序     号	1	2	3	4	5	6	7	8	9	10
身高x(厘米)	192	164	172	177	176	159	171	166	182	166
脚长y( 码 )	48	38	40	43	44	37	40	39	46	39
序     号	11	12	13	14	15	16	17	18	19	20
身高x(厘米)	169	178	167	174	168	179	165	170	162	170
脚长y( 码 )	43	41	40	43	40	44	38	42	39	41

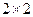(Ⅰ)若“身高大于175厘米”的为“高个”，“身高小于等于175厘米”的为“非高个”；“脚长大于42码”的为“大脚”，“脚长小于等于42码”的为“非大脚”.请根据上表数据完成下面的联黑框列表: (3分)

	高 个	非高个	合 计
大 脚
非大脚		12
合 计			20

   (Ⅱ) 若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有数字1，2，3，4，5，6的正六面体骰子连续投掷两次，记朝上的两个数字的乘积为被抽取人的序号.试求:
①抽到12号的概率；②抽到“无效序号(超过20号)”的概率. (6分)
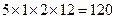(Ⅲ) 根据题(1)中表格的数据，若按99.5%的可靠性要求，能否认为脚的大小与身高之间有关系?（可用数据48²＝2304、58²＝3364、68²＝4624、 、 ）(5分)

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

第Ⅰ卷

一、填空题:

1. {1,2,3}; 2.充分非必要;3.; 4.;  5. 8;  6. (历史) 5049; (物理) ; 7. 1; 8.

9.;10.; 11.; 12.;13.;14. 4.

二、解答题：

15. 解：（1）因为,所以…………（3分）

     得 （用辅助角得到同样给分）              ………（5分）

     又,所以=           ……………………………………（7分）

（2）因为    ………………………（9分）

=                     …………………………………………（11分）

所以当=时, 的最大值为5＋4=9               …………………（13分）

故的最大值为3                     ………………………………………（14分）

16. (选历史方向) 解: （1）表格为:

高  个

非高个

合  计

大  脚

5

2

7

非大脚

1

13

合  计

6

14

…… （3分）

（说明:黑框内的三个数据每个1分,黑框外合计数据有错误的暂不扣分）

（2）提出假设H₀: 人的脚的大小与身高之间没有关系. …………………………… （4分）

根据上述列联表可以求得.…………………… （7分）

当H₀成立时,的概率约为0.005,而这里8.802>7.879,

所以我们有99.5%的把握认为: 人的脚的大小与身高之间有关系. ……………… （8分）

（3） ①抽到12号的概率为………………………………… （11分）

②抽到“无效序号（超过20号）”的概率为…………………… （14分）

(选物理方向) 解：（Ⅰ）在给定的直角坐标系下，设最高点为A，入水点为B，

抛物线的解析式为． …………………………… 2′

由题意，知O（0，0），B（2，－10），且顶点A的纵坐标为．……………   4′

或        …………………………… 8′

∵抛物线对称轴在y轴右侧，∴,又∵抛物线开口向下，∴a＜0,

从而b＞0,故有       ……………………………9′           

∴抛物线的解析式为.   ……………………………10′

（Ⅱ）当运动员在空中距池边的水平距离为米时，

即时，， ……………………………12′

∴此时运动员距水面的高为10－＝＜5，因此，此次跳水会失误.………………14′

17. （1）证明：由直四棱柱,得,

所以是平行四边形,所以         …………………（3分）

而,,所以面  ………（4分）

（2）证明：因为, 所以       ……（6分）

又因为,且，所以    ……… ……（8分）

而，所以               …………………………（9分）

（3）当点为棱的中点时,平面平面…………………（10分）

取DC的中点N,,连结交于,连结.

因为N是DC中点,BD=BC,所以；又因为DC是面ABCD与面的交线,而面ABCD⊥面,

所以……………（12分）

又可证得,是的中点,所以BM∥ON且BM=ON,即BMON是平行四边形,所以BN∥OM,所以OM平面,

因为OM?面DMC₁,所以平面平面………………………（14分）

18. 解：（1）因为,所以c=1……………………（2分）

 则b=1,即椭圆的标准方程为…………………………（4分）

（2）因为（1,1）,所以,所以,所以直线OQ的方程为y=－2x（6分）

又椭圆的左准线方程为x=－2,所以点Q（－2,4） …………………………（7分）

所以,又,所以,即,

故直线与圆相切……………………………………………………（9分）

（3）当点在圆上运动时,直线与圆保持相切              ………（10分）

证明:设（）,则,所以,,

所以直线OQ的方程为                     ……………（12分）

所以点Q（－2,）                                    ……………… （13分）

所以,

又,所以,即,故直线始终与圆相切……（15分）

19.⑴解：函数的定义域为，（）…… （2分）

若，则，有单调递增区间． ……………… （3分）

若，令，得，      

当时，，

当时，．  ……………… （5分）

有单调递减区间，单调递增区间．   ……………… （6分）

⑵解:(i)若，在上单调递增，所以．     ……… （7分）

若，在上单调递减，在上单调递增，

所以．     ……………… （9分）

若，在上单调递减，所以．………… （10分）

综上所述，    ……………… （12分）

（ii）令．若，无解．      ……………… （13分）

若，解得． ……………… （14分）

若，解得．       ……………… （15分）

故的取值范围为．    ……………… （16分）

20. (1)数表中第行的数依次所组成数列的通项为，则由题意可得

… （2分）

 (其中为第行数所组成的数列的公差)         (4分)

(2)

第一行的数依次成等差数列，由(1)知，第2行的数也依次成等差数列，依次类推，可知数表中任一行的数(不少于3个)都依次成等差数列.     ……………… （5分）

设第行的数公差为,则，则…………… （6分）

所以

                                           (10 分)

(3)由，可得

所以=   ……………… （11分）

令,则,所以 ………… （13分）

要使得，即，只要=，

，，所以只要,

即只要,所以可以令

则当时，都有.

所以适合题设的一个函数为                   (16分)

第Ⅱ卷（附加题 共40分）

1. （1）设动点P的坐标为,M的坐标为,

则即为所求的轨迹方程.  …………（6分）

（2）由（1）知P的轨迹是以（）为圆心，半径为的圆，易得RP的最小值为1

.……（10分）

2. ，|x－a|＜l，

，       …………………………………………………5分

= ………………………10分

3. 证明：以为坐标原点长为单位长度，如图建立空间直角坐标系，则各点坐标为

．

（1）解：因

所以，与所成的角余弦值为     …………………………………5分

（2）解：在上取一点，则存在使