
题目列表(包括答案和解析)
| 所用的时间(天数) | 10 | 11 | 12 | 13 |
| 通过公路1的频数 | 20 | 40 | 20 | 20 |
| 通过公路2的频数 | 10 | 40 | 40 | 10 |
 将数列{an}中的所有项按每一行比上一行多一项的规则排成如下表:
将数列{an}中的所有项按每一行比上一行多一项的规则排成如下表: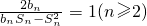 .
.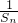 成等差数列,并求数列{bn}的通项公式;
成等差数列,并求数列{bn}的通项公式;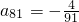 时,公比q的值.
时,公比q的值.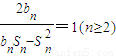 .
.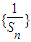 成等差数列,并求数列{bn}的通项公式;
成等差数列,并求数列{bn}的通项公式;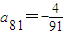 时,公比q的值.
时,公比q的值.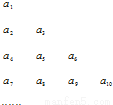
 .
. 成等差数列,并求数列{bn}的通项公式;
成等差数列,并求数列{bn}的通项公式; 时,公比q的值.
时,公比q的值.
 某城市自西向东和自南向北的两条主干道的东南方位有一块空地,市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,其中,Ox,Oy分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点O处修一条步行小道,小道为抛物线y=x2的一段,在小道上依次以点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(n≥10,n∈N*)为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn.
某城市自西向东和自南向北的两条主干道的东南方位有一块空地,市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,其中,Ox,Oy分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点O处修一条步行小道,小道为抛物线y=x2的一段,在小道上依次以点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(n≥10,n∈N*)为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn.| 1 |
| xn |
| πS |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com