“已知：中，，求证：”。下面写出了用反证法证明这个命题过程中的四个推理步骤：
（1）所以，这与三角形内角和定理相矛盾，；
（2）所以；
（3）假设；
（4）那么，由，得，即
这四个步骤正确的顺序应是

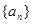数列，满足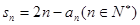

（1）求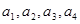，并猜想通项公式。

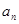（2）用数学归纳法证明（1）中的猜想。

【解析】本试题主要考查了数列的通项公式求解，并用数学归纳法加以证明。第一问利用递推关系式得到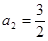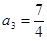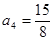，，，，并猜想通项公式

第二问中，用数学归纳法证明（1）中的猜想。

①对n=1，等式成立。

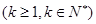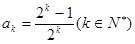②假设n=k时，成立，

那么当n=k+1时，

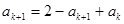，所以当n=k+1时结论成立可证。

数列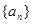，满足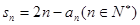

（1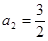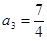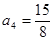），，，并猜想通项公。  …4分

（2）用数学归纳法证明（1）中的猜想。①对n=1，等式成立。  …5分

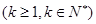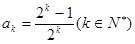②假设n=k时，成立，

那么当n=k+1时，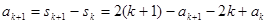

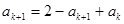，             ……9分

所以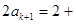

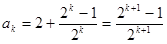
所以当n=k+1时结论成立                     ……11分

由①②知，猜想对一切自然数n均成立

“已知：中，，求证：”。下面写出了用反证法证明这个命题过程中的四个推理步骤：

（1）所以，这与三角形内角和定理相矛盾，；

（2）所以；

（3）假设；

（4）那么，由，得，即

这四个步骤正确的顺序应是

A．（1）（2）（3）（4） B．（3）（4）（2）（1）  C．（3）（4）（1）（2） D．（3）（4）（2）（1）

（07年北京卷理）已知集合，其中，由中的元素构成两个相应的集合：

，．

其中是有序数对，集合和中的元素个数分别为和．

若对于任意的，总有，则称集合具有性质．

（I）检验集合与是否具有性质并对其中具有性质的集合，写出相应的集合和；

（II）对任何具有性质的集合，证明：；

（III）判断和的大小关系，并证明你的结论．