
题目列表(包括答案和解析)
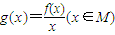 的零点个数.
的零点个数.| f(x) |
| x |
| f(x) | x |
1-10.CDBBA CACBD
11. 12. ①③④ 13.-2或1 14.
12. ①③④ 13.-2或1 14.  、
、 15.2 16.
15.2 16.  17.
17. .
.
18.
解:(1)由已知
 7分
7分
(2)由 10分
10分
由余弦定理得 14分
14分
19.(1)证明:∵PA⊥底面ABCD,BC 平面AC,∴PA⊥BC, 3分
平面AC,∴PA⊥BC, 3分
∵∠ACB=90°,∴BC⊥AC,又PA∩AC=A,∴BC⊥平面PAC. 5分
(2)解:过C作CE⊥AB于E,连接PE,
∵PA⊥底面ABCD,∴CE⊥面PAB,
∴直线PC与平面PAB所成的角为 , 10分
, 10分
∵AD=CD=1,∠ADC=60°,∴AC=1,PC=2,
 中求得CE=
中求得CE= ,∴
,∴ . 14分
. 14分
 20.解:(1)由
20.解:(1)由 ①,得
①,得 ②,
②,
②-①得: . 4分
. 4分
(2)由 求得
求得 . 7分
. 7分
∴ ,
, 11分
11分

∴ .
14分
.
14分
21.解:
(1)由 得c=1 1分
得c=1 1分
 , 4分
, 4分
|