
题目列表(包括答案和解析)
①命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”;
②若P且Q为假命题,则P、Q均为假命题;
③在△ABC中,sinA>sinB的充要条件是A>B;
④不等式的解集为|x|+|x-1|>a的解集为R,则a≤1;
⑤点(x,y)在映射f作用下的象是(2x,![]() ),则在f的作用下,点(1,-1)的原象是(0,2).其中真命题的是________(写出所有真命题的编号)
),则在f的作用下,点(1,-1)的原象是(0,2).其中真命题的是________(写出所有真命题的编号)
| x2 |
| 2-m |
| y2 |
| m2-4 |
| x2 |
| 45 |
| y2 |
| 20 |
| x2 |
| 10-m |
| y2 |
| 6-m |
| x2 |
| 5-m |
| y2 |
| 9-m |
| b |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 4a |
|
给出下列命题:
①命题“所有的正方形都是矩形”的否定是“所有的正方形都不是矩形”;
②设p、q 为简单命题,则“p且q”为假是“p或q为假的必要而不充分条件;
③函数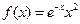 的极小值为
的极小值为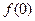 ,极大
,极大 值为
值为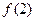 ;
;
④双曲线的渐近线方程是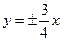 ,则该双曲线的离心率是
,则该双曲线的离心率是 .
.
⑤等差数列
 中首项为
中首项为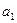 ,则数列
,则数列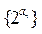 为等比数列;
为等比数列;
其中真命题的序号为 (写出所有真命题的序号)
一、选择题(每小题5分,共50分)

二、填空题(每小题4分,共28分)

三、解答题
18.解:(Ⅰ)由已有



(4分)

(6分)
(Ⅱ)由(1) 且
且 (8分)
(8分)
所以 (10分)
(10分)
 (12分)
(12分)

 (14分)
(14分)
19.解:(Ⅰ)同学甲同学恰好投4次达标的概率 (4分)
(4分)
(Ⅱ) 可取的值是
可取的值是
 (6分)
(6分)
 (8分)
(8分)
 (10分)
(10分)
 的分布列为
的分布列为

3
4
5



(12分)
所以 的数学期望为
的数学期望为 (14分)
(14分)
20.解:(Ⅰ)∵PA⊥底面ABCD,BC 平面AC,∴PA⊥BC
平面AC,∴PA⊥BC
∵∠ACB=90°,∴BC⊥AC,又PA∩AC=A,∴BC⊥平面PAC (4分)
(Ⅱ)取CD的中点E,则AE⊥CD,∴AE⊥AB,又PA⊥底面ABCD,∴PA⊥AE
建立如图所示空间直角坐标系,则
A(0,,0,0),P(0,0, ),C(
),C( ,0),D(
,0),D( ,0)
,0)

 ,
, ,
, (6分)
(6分)
易求 为平面PAC的一个法向量.
为平面PAC的一个法向量.
 为平面PDC的一个法向量
(9分)
为平面PDC的一个法向量
(9分)
∴cos
故二面角D-PC-A的正切值为2. (11分)
(Ⅲ)设 ,则
,则
 ,
,
解得点 ,即
,即 (13分)
(13分)
由 得
得 (不合题意舍去)或
(不合题意舍去)或
所以当 为
为 的中点时,直线
的中点时,直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 (15分)
(15分)
21.解:(Ⅰ)设直线 的方程为:
的方程为:
由 得
得 ,所以
,所以 的方程为
的方程为 (4分)
(4分)
由 得
得 点的坐标为
点的坐标为 .
.
可求得抛物线的标准方程为 .
(6分)
.
(6分)
(Ⅱ)设直线 的方程为
的方程为 ,代入抛物线方程并整理得
,代入抛物线方程并整理得 (8分)
(8分)
设 则
则
设 ,则
,则



 (11分)
(11分)
当 时上式是一个与
时上式是一个与 无关的常数.
无关的常数.
所以存在定点 ,相应的常数是
,相应的常数是 .
(14分)
.
(14分)
22.解:(Ⅰ)当 时
时 (2分)
(2分)
 在
在 上递增,在
上递增,在 上递减
上递减
所以 在0和2处分别达到极大和极小,由已知有
在0和2处分别达到极大和极小,由已知有
 且
且 ,因而
,因而 的取值范围是
的取值范围是 .
(4分)
.
(4分)
(Ⅱ)当 时,
时, 即
即
|