
题目列表(包括答案和解析)
(甲)在三棱柱 中,
中,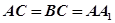 ,
, 分别是
分别是 的中点, G是
的中点, G是 上的点,
上的点,
(1)如果 ,试确定点
,试确定点 的位置;
的位置;
(2)在满足条件(1)的情况下,试求 的值。
的值。

(乙)正方体 中,
中,
(1)在棱 上有一点
上有一点 ,当
,当 为多少时,使二面角
为多少时,使二面角 的大小等于
的大小等于 ;
;
(2)在(1)的条件下,求直线 所成的角。
所成的角。

[来源:.COM]
如图,在直三棱柱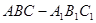 中,
中, ,
,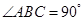 ,
,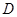 是
是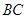 的中点.
的中点.
(Ⅰ)求证: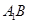 ∥平面
∥平面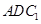 ; (Ⅱ)求二面角
; (Ⅱ)求二面角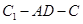 的余弦值;
的余弦值;
(Ⅲ)(理科)试问线段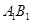 上是否存在点
上是否存在点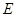 ,使
,使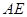 与
与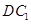 成
成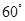 角?若存在,确定
角?若存在,确定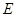 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.
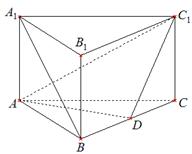
如图,在直三棱柱 中,
中, ,
, ,
, 是
是 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)试问线段 上是否存在点
上是否存在点 ,使
,使 与
与 成
成 角?若存在,确定
角?若存在,确定 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.

如图,在直三棱柱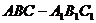 中,
中,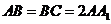 ,
,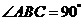 ,
,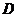 是
是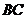 的中点.
的中点.
(Ⅰ)求证: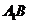 ∥平面
∥平面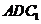 ; (Ⅱ)求二面角
; (Ⅱ)求二面角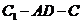 的余弦值;
的余弦值;
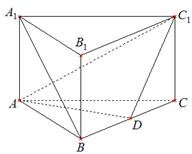 (Ⅲ)(理科)试问线段
(Ⅲ)(理科)试问线段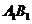 上是否存在点
上是否存在点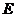 ,使
,使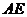 与
与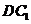 成
成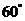 角?若存在,确定
角?若存在,确定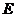 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.
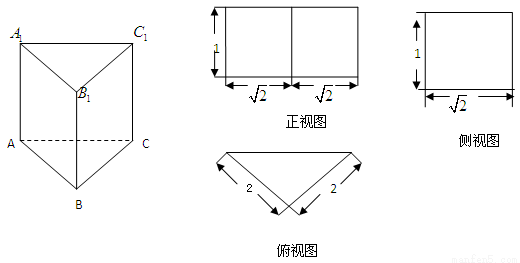
已知直三棱柱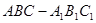 的三视图如图所示,
的三视图如图所示,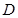 是
是 的中点.
的中点.
(Ⅰ)求证: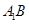 ∥平面
∥平面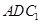 ;
;
(Ⅱ)求二面角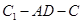 的余弦值;
的余弦值;
(Ⅲ)试问线段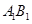 上是否存在点
上是否存在点 ,使
,使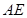 与
与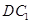 成
成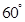 角?若存在,确定
角?若存在,确定 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.
一、选择题(每小题5分,共50分)

二、填空题(每小题4分,共28分)

三、解答题
18.解:(Ⅰ)由已有



(4分)

(6分)
(Ⅱ)由(1) 且
且 (8分)
(8分)
所以 (10分)
(10分)
 (12分)
(12分)

 (14分)
(14分)
19.解:(Ⅰ)同学甲同学恰好投4次达标的概率 (4分)
(4分)
(Ⅱ) 可取的值是
可取的值是
 (6分)
(6分)
 (8分)
(8分)
 (10分)
(10分)
 的分布列为
的分布列为

3
4
5



(12分)
所以 的数学期望为
的数学期望为 (14分)
(14分)
20.解:(Ⅰ)∵PA⊥底面ABCD,BC 平面AC,∴PA⊥BC
平面AC,∴PA⊥BC
∵∠ACB=90°,∴BC⊥AC,又PA∩AC=A,∴BC⊥平面PAC (4分)
(Ⅱ)取CD的中点E,则AE⊥CD,∴AE⊥AB,又PA⊥底面ABCD,∴PA⊥AE
建立如图所示空间直角坐标系,则
A(0,,0,0),P(0,0, ),C(
),C( ,0),D(
,0),D( ,0)
,0)

 ,
, ,
, (6分)
(6分)
易求 为平面PAC的一个法向量.
为平面PAC的一个法向量.
 为平面PDC的一个法向量
(9分)
为平面PDC的一个法向量
(9分)
∴cos
故二面角D-PC-A的正切值为2. (11分)
(Ⅲ)设 ,则
,则
 ,
,
解得点 ,即
,即 (13分)
(13分)
由 得
得 (不合题意舍去)或
(不合题意舍去)或
所以当 为
为 的中点时,直线
的中点时,直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 (15分)
(15分)
21.解:(Ⅰ)设直线 的方程为:
的方程为:
由 得
得 ,所以
,所以 的方程为
的方程为 (4分)
(4分)
由 得
得 点的坐标为
点的坐标为 .
.
可求得抛物线的标准方程为 .
(6分)
.
(6分)
(Ⅱ)设直线 的方程为
的方程为 ,代入抛物线方程并整理得
,代入抛物线方程并整理得 (8分)
(8分)
设 则
则
设 ,则
,则



 (11分)
(11分)
当 时上式是一个与
时上式是一个与 无关的常数.
无关的常数.
所以存在定点 ,相应的常数是
,相应的常数是 .
(14分)
.
(14分)
22.解:(Ⅰ)当 时
时 (2分)
(2分)
 在
在 上递增,在
上递增,在 上递减
上递减
所以 在0和2处分别达到极大和极小,由已知有
在0和2处分别达到极大和极小,由已知有
 且
且 ,因而
,因而 的取值范围是
的取值范围是 .
(4分)
.
(4分)
(Ⅱ)当 时,
时, 即
即
|