练习册

  • 练习册
  • 试题
    16．班主任准备从班上10名男团员.6名女团员中选3人组成一个主委组.则选到的3名同学中既有男团员又有女团员的不同选法共有 种 【查看更多】

     

    题目列表(包括答案和解析)

    精英家教网某学校为了了解高三学生月考的数学成绩，从甲、乙两班各抽取10名学生，并统计他们的成绩（成绩均为整数且满分为100分），成绩如下：
    甲班：97，81，91，80，89，79，92，83，85，93
    乙班：60，80，87，77，96，64，76，60，84，96
    （Ⅰ）根据抽取结果填写茎叶图，并根据所填写的茎叶图，对甲、乙两班的成绩做对比，写出两个统计结论；
    （Ⅱ）若可计算得抽取甲班的10名学生的数学成绩的平均值为
    .
    		x
    =87    ，将10名甲班学生的数学成绩依次输入，按程序框图进行运算，问输出的S大小为多少？并说明S的统计学意义；
    （Ⅲ）学校规定成绩在90分以上为优秀，现准备从甲、乙两班所抽取的学生中选取两名成绩为优秀的学生参加数学竞赛，求至少有一名乙班学生参加数学竞赛的概率．

    查看答案和解析>>

    某学校为了了解高三学生月考的数学成绩，从甲、乙两班各抽取10名学生，并统计他们的成绩（成绩均为整数且满分为100分），成绩如下：
    甲班：97，81，91，80，89，79，92，83，85，93
    乙班：60，80，87，77，96，64，76，60，84，96
    （Ⅰ）根据抽取结果填写茎叶图，并根据所填写的茎叶图，对甲、乙两班的成绩做对比，写出两个统计结论；
    （Ⅱ）若可计算得抽取甲班的10名学生的数学成绩的平均值为，将10名甲班学生的数学成绩依次输入，按程序框图进行运算，问输出的S大小为多少？并说明S的统计学意义；
    （Ⅲ）学校规定成绩在90分以上为优秀，现准备从甲、乙两班所抽取的学生中选取两名成绩为优秀的学生参加数学竞赛，求至少有一名乙班学生参加数学竞赛的概率．

    查看答案和解析>>

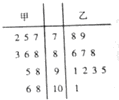    从甲、乙两个班级各随机抽取10名同学的数学成绩进行统计分析，两班成绩的茎叶图如图所示，成绩不小于90分为及格．
    （I）试完成甲班制取10名同学数学成绩频率分布表，并估计甲班的及格率．
    分组 频数 频率
    [70，80）
    [80，90）
    [90，100）
    [100，110）
    （II）从每班抽取的同学中各抽取一人，求至少有一人及格的概率．

    查看答案和解析>>

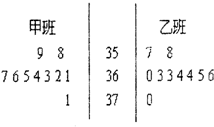    为检测学生的体温状况，随机抽取甲，乙两个班各10名同学，测量他们的体温（单位0.1摄氏度）获得体温数据的茎叶图，如图所示．
    （1）计算乙班的样本平均数，方差；
    （2）现在从甲班中随机抽取两名体温不低于36.5摄氏度的同学，求体温为37.1摄氏度的同学被抽到的概率．

    查看答案和解析>>

    随机抽取某中学甲乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图．
    （1）根据茎叶图判断哪个班的平均身高较高；
    （2）计算甲班的样本方差；
    （3）现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，求身高为176cm的同学被抽中的概率．

    查看答案和解析>>

     

    一、选择题（本大题共12个小题，每小题5分，共60分）

        1―5  BCBAB    6―10  CDBDD   11―12AB

    20090323

    13．9

    14．

    15．（1，0）

    16．420

    三、解答题：

    17．解：（1）

       （2）由（1）知，

           

    18．解：设“通过第一关”为事件A1，“补过且通过第一关”为事件A2，“通过第二关”为事件B1，“补过且通过第二关”为事件B2。             （2分）

       （1）不需要补过就可获得奖品的事件为A=A1?B1，又A1与B1相互独立，则P（A）=P

    （A1?B1）=P（A1）?P（B1）=。故他不需要补过就可获得奖品的概率为。

    （6分）

       （2）由已知得ξ=2，3，4，注意到各事件之间的独立性与互斥性，可得

           

    19．解法：1：（1）

       （2）过E作EF⊥PC，垂足为F，连结DF。             （8分）

    由Rt△EFC∽

    解法2：（1）

       （2）设平面PCD的法向量为

            则

               解得   

    AC的法向量取为

     角A―PC―D的大小为

    20．（1）由已知得    

      是以a2为首项，以

        （6分）

       （2）证明：

       

    21：解（1）由线方程x+2y+10-6ln2=0知，

        直线斜率为

      

        所以   解得a=4，b=3。    （6分）

       （2）由（1）得

    令

    22．解：（1）设直线l的方程为

    得因为直线l与椭圆交点在y轴右侧，

    所以  解得2

    故l直线y截距的取值范围为。          （4分）

       （2）①（Ⅰ）当AB所在的直线斜率存在且不为零时，

    设AB所在直线方程为

    解方程组           得

    所以

    设

    所以

    因为l′是AB的垂直平分线，所以直线l′的方程为

     

    因此

     又

       （Ⅱ）当k=0或不存在时，上式仍然成立。

    综上所述，M的轨迹方程为（λ≠0）。  （9分）

    ②当k存在且k≠0时，由（1）得

    由  解得

    所以

    解法：（1）由于

    当且仅当4+5k2=5+4k2，即k≠±1时等号成立，

    此时，

     

    当

    当k不存在时，

    综上所述，                      （14分）

    解法（2）：

    因为

    又

    当且仅当4+5k2=5+4k2，即k≠±1时等号成立，

    此时。

    当

    当k不存在时，

    综上所述，。

     

     

     

     


    同步练习册答案