
题目列表(包括答案和解析)
(本小题满分10分)某食品厂定期购买面粉,已知该厂每天需用面粉6吨,每吨面粉的价格为1800元,面粉的保管等其他费用为平均每吨3元,购面粉每次需支付运费900元。
(1)求该厂多少天购买一次面粉,才能使平均每天所支付的总费用最少?
(2)若提供面粉的公司规定:当一次购买面粉不少于210吨时,其价格可享受九折优惠,问该厂是否考虑利用此优惠条件?请说明理由。
(本小题满分13分)
由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高.然而也有部分公众对该活动的实际效果与负面影响提出了疑问.对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| 支持 | 保留 | 不支持 | |
| 20岁以下 | 800 | 450 | 200 |
| 20岁以上(含20岁) | 100 | 150 | 300 |
(Ⅰ)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从“支持”态度的人中抽取了45人,求
个人,已知从“支持”态度的人中抽取了45人,求![]() 的值;
的值;
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任意选取2人,求至少有![]() 人20岁以下的概率;
人20岁以下的概率;
(Ⅲ)在接受调查的人中,有8人给这项活动打出的分数如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8个人打出的分数看作一个总体,从中任取![]() 个数,求该数与总体平均数之差的绝对值超过0.6的概率.
个数,求该数与总体平均数之差的绝对值超过0.6的概率.
 .记小球遇到第n行第m个障碍物(从左至右)上顶点的概率为P(n,m).
.记小球遇到第n行第m个障碍物(从左至右)上顶点的概率为P(n,m).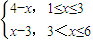 ,设小球遇到第6行第m个障碍物(从左至右)上顶点时,得到的分数为ξ=f(m),试求ξ的分布列及数学期望.
,设小球遇到第6行第m个障碍物(从左至右)上顶点时,得到的分数为ξ=f(m),试求ξ的分布列及数学期望.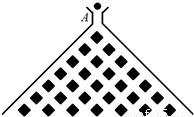
 .记小球遇到第n行第m个障碍物(从左至右)上顶点的概率为P(n,m).
.记小球遇到第n行第m个障碍物(从左至右)上顶点的概率为P(n,m).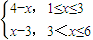 ,设小球遇到第6行第m个障碍物(从左至右)上顶点时,得到的分数为ξ=f(m),试求ξ的分布列及数学期望.
,设小球遇到第6行第m个障碍物(从左至右)上顶点时,得到的分数为ξ=f(m),试求ξ的分布列及数学期望.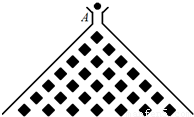
 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)| 5 |
|
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com