
题目列表(包括答案和解析)
| 2x-1 |
| x |
| x |
| 2x-1 |
| 2x-1 |
| x |
| 2x-1 |
| x |
| 2x-1 |
| x |
| 12 |
| x2-2x |
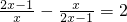 时,如果设
时,如果设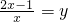 ,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成
,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成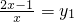 和
和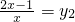 ,即可解出x1和x2.请用换元法解方程:
,即可解出x1和x2.请用换元法解方程: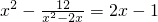 .
. 时,如果设
时,如果设 ,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成
,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成 和
和 ,即可解出x1和x2.请用换元法解方程:
,即可解出x1和x2.请用换元法解方程: .
.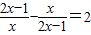 时,如果设
时,如果设 ,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成
,并将原方程化为关于y的整式方程,那么这个整式方程是y2-2y-1=0,然后在解出y1和y2,再将y1和y2替换成 和
和 ,即可解出x1和x2.请用换元法解方程:
,即可解出x1和x2.请用换元法解方程: .
.在日常生活中如取款、上网等都需要密码. 有一种用 “因式分解” 法产生的密码, 方便记忆. 原理是: 如对于多项式x4-y4, 因式分解的结果是(x-y)(x+y)(x2+y2). 若取x=9,y=9时, 则各个因式的值是: (x-y)=0, (x+y)=18, (x2+y2)=162, 于是就可以把 “018162” 作为一个六位数的密码. 对于多项式25(x+2y)2-4(x-y)2, 取x=10,y=10时, 用上述方法产生的密码是: _________________________(写出一个即可)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com