练习册

  • 练习册
  • 试题
    已知.函数 【查看更多】

     

    题目列表(包括答案和解析)

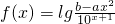    已知数学公式，函数y=f（x）与函数y=g（x）满足如下对应关系：当点（x，y）在y=f（x）的图象上时，点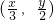数学公式在y=g（x）的图象上，且f（0）=0，g（-1）=1．
    （1）求函数y=g（x）的解析式；
    （2）指出函数y=g（x）的单调递增区间，并用单调性定义证明之．

    查看答案和解析>>

    已知，函数的．

    (1)求的值．

    (2)求函数．

    查看答案和解析>>

    （12分）已知，函数，（为自然对数的底数）

    （I）当时，求函数的单调递增区间；

    （Ⅱ）若函数在（-1，1）上单调递增，求的取值范围；

    （Ⅲ）函数能否为上的单调函数？若能，求出的取值范围；若不能，请说明理由。

    查看答案和解析>>

    已知，函数，在是一个单调函数。

    （1）试问在的条件下，在能否是单调递减函数？说明理由。

    （2）若在上是单调递增函数，求实数a的取值范围。

    （3）设且，比较与的大小。

    查看答案和解析>>

    已知，函数，当时，.（1）求常数的值

    （2）设，求的单调区间

    查看答案和解析>>

    说明：

        一、本解答给出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则。

    二、对计算题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定后续部分的给分，但不得超过该部分正确解答所给分数的一半；如果后续部分的解答存在较严重的错误，则不再给分。

    三、解答右端所注分数，表示考生正确做到这一步应得的累加分数。

    四、每题只给整数分数，选择题和填空题不给中间分。

    一、选择题：

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    答案

    B

    C

    C

    D

    A

    A

    B

    C

    B

    D

    二、填空题：

    11．40.6,1.1  12． 13． 14．30  15．  16．（1，1），（2，2），（3，4），（4，8）

    三、解答题：

      17．（Ⅰ），                         ①            …………………2分

        又， ∴                 ②             ……………… 4分

        由①、②得              …………………………………………………………… 6分

       （Ⅱ）  ……………………………………… 8分

                     …………………………………………………………………… 10分

         …………………………………………………………………………12分

    18．（Ⅰ）设点，则，

    ，

    ，又，

    ，∴椭圆的方程为：    …………………………………………7分

    （Ⅱ）当过直线的斜率不存在时，点，则；

         当过直线的斜率存在时，设斜率为，则直线的方程为，

    设，由    得：

           …………………………………………10分

     

                                               ……13分

    综合以上情形，得：    ……………………………………………………14分

    ∴GH∥AD∥EF，∴E，F，G，H四点共面. ……………………1分

    又H为AB中点，∴EH∥PB. 又EH面EFG，PB平面EFG，

    ∴PB∥平面EFG.                 ………………………………4分

       （Ⅱ）取BC的中点M，连结GM、AM、EM，则GM//BD，

    ∴∠EGM（或其补角）就是异面直线EG与BD所成的角.……6分

         在Rt△MAE中， ，

         同理，又GM=，………………7分

    ∴在△MGE中，     ………………8分

    故异面直线EG与BD所成的角为arccos，                   ………………………………9分

    又AB∩PA=A，∴AD⊥平面PAB. ……………………………………10分

    又∵E，F分别是PA，PD中点，∴EF∥AD，∴EF⊥平面PAB.   

    又EF面EFQ，∴面EFQ⊥面PAB. ………………………………11分

    过A作AT⊥ER于T，则AT⊥平面EFQ，

    ∴AT就是点A到平面EFQ的距离. ………………………………12分

    设，则

        在，            …………………………13分

         解得 故存在点Q，当CQ=时，点A到平面EFQ的距离为0.8. ……………………… 14分

    解法二：建立如图所示的空间直角坐标系A－xyz，则A（0，0，0），B（2，0，0），C（2，2，0），D（0，2，0），

       （Ⅰ） …………1分

        设，  即，

       

                  ……………3分

        ，∴PB∥平面EFG. ………………………………………………………… 4分

       （Ⅱ）∵,              …………………………………………5分

        ，            ……………………… 8分

    故异面直线EG与BD所成的角为arcos.            …………………………………… 9分

       （Ⅲ）假设线段CD上存在一点Q满足题设条件，令

        ∴点Q的坐标为（2－m，2，0）， ……………………………………10分

        而， 设平面EFQ的法向量为，则

         

        令，             ……………………………………………………12分

        又， ∴点A到平面EFQ的距离，……13分

        即，不合题意，舍去.

        故存在点Q，当CQ=时，点A到平面EFQ的距离为0.8.           ……………………14分

    20． (Ⅰ)，          ………………2分

    当时，，        …………4分

       （Ⅱ）是单调增函数；   ………………6分

    由是单调减函数；      ………………8分

       （Ⅲ）是偶函数，对任意都有成立

    *  对任意都有成立

    1°由（Ⅱ）知当或时，是定义域上的单调函数，

    对任意都有成立

    时，对任意都有成立                   …………10分

    2°当时，，由

    上是单调增函数在上是单调减函数，∴对任意都有

    时，对任意都有成立               ………………12分

    综上可知，当时，对任意都有成立           .……14分

    21、（Ⅰ）设等差数列{}的公差是，则，解得

    所以                ……………………………………2分

    由=－1＜0

    得适合条件①；又，所以当=4或5时，取得最大值20，即≤20，适合条件②。综上所述， …………………………………………4分

    （Ⅱ）因为，所以当n≥3时，，此时数列单调递减；当=1，2时，，即

    因此数列中的最大项是，所以≥7………………………………………………………8分

    （Ⅲ）假设存在正整数，使得成立，

    由数列的各项均为正整数，可得                ……………10分

    因为                 ……11分

    由              …13分

    因为

    依次类推，可得            ……………………………………………15分

    又存在，使，总有，故有，这与数列（）的各项均为正整数矛盾！

    所以假设不成立，即对于任意,都有成立.           ………………………16分

     


    同步练习册答案