练习册

  • 练习册
  • 试题
    解(1):△ABC的内角为A+B+C= 【查看更多】

     

    题目列表(包括答案和解析)

    △ABC的内角A、B、C的对边分别为a、b、c，已知cos（A-C）＋cosB=1，a=2c，求c

    【解析】解：因为

     

    查看答案和解析>>

    已知△ABC的内角A，B，C的对边分别为a，b，c，下列说法中：①在△ABC中，a=x，b=2，B=45°，若该三角形有两解，则x取值范围是2＜x＜2
    		2
    ；②在△ABC中，若b=8，c=5，A=60°，则△ABC的外接圆半径等于
    14
    		3
    3
    ；③在△ABC中，若c=5，
    cosA
    cosB
    =
    b
    a
    =
    4
    3
    ，则△ABC的内切圆的半径为2；④在△ABC中，若AB=4，AC=7，BC=9，则BC边的中线AD=
    7
    2
    ；⑤设三角形ABC的BC边上的高AD=BC，a、b、c分别表示角A、B、C对应的三边，则
    b
    c
    +
    c
    b
    的取值范围是[2，
    		5
    ]    ．其中正确说法的序号是
    ①④⑤
    ①④⑤
    （注：把你认为是正确的序号都填上）．

    查看答案和解析>>

    已知△ABC的内角A，B，C的对边分别为a，b，c，下列说法中：①在△ABC中，a=x，b=2，B=45°，若该三角形有两解，则x取值范围是2＜x＜2
    		2
    ；②在△ABC中，若b=8，c=5，A=60°，则△ABC的外接圆半径等于
    14
    		3
    3
    ；③在△ABC中，若c=5，
    cosA
    cosB
    =
    b
    a
    =
    4
    3
    ，则△ABC的内切圆的半径为2；④在△ABC中，若AB=4，AC=7，BC=9，则BC边的中线AD=
    7
    2
    ；⑤设三角形ABC的BC边上的高AD=BC，a、b、c分别表示角A、B、C对应的三边，则
    b
    c
    +
    c
    b
    的取值范围是[2，
    		5
    ]    ．其中正确说法的序号是______（注：把你认为是正确的序号都填上）．

    查看答案和解析>>

    已知△ABC的内角A，B，C的对边分别为a，b，c，下列说法中：①在△ABC中，a=x，b=2，B=45°，若该三角形有两解，则x取值范围是；②在△ABC中，若b=8，c=5，A=60°，则△ABC的外接圆半径等于；③在△ABC中，若c=5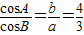，，则△ABC的内切圆的半径为2；④在△ABC中，若AB=4，AC=7，BC=9，则BC边的中线；⑤设三角形ABC的BC边上的高AD=BC，a、b、c分别表示角A、B、C对应的三边，则的取值范围是．其中正确说法的序号是    （注：把你认为是正确的序号都填上）．

    查看答案和解析>>

    已知△ABC的三个内角A、B、C所对的边分别为a、b、c，向量

    （Ⅰ）求角A的大小；

    （Ⅱ）若，试判断b·c取得最大值时△ABC形状.

    【解析】本试题主要考查了解三角形的运用。第一问中利用向量的数量积公式，且由

    （2）问中利用余弦定理，以及，可知，并为等边三角形。

    解：(Ⅰ)

         ………………………………6分

    (Ⅱ)

    ………………………………8分

    ……………10分

     

    查看答案和解析>>


    同步练习册答案