
题目列表(包括答案和解析)
阅读材料:(本题8分)
例:说明代数式  的几何意义,并求它的最小值.
的几何意义,并求它的最小值.
解:  ,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则
,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则 可以看成点P与点A(0,1)的距离,
可以看成点P与点A(0,1)的距离,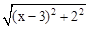 可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,
只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,
所以PA′+PB的最小值为线段A′B的长度.为此,构造直角
三角形A′CB,因为A′C=3,CB=3,所以A′B=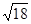 ,
,
即原式的最小值为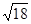 。
。
根据以上阅读材料,解答下列问题:
(1)代数式 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标)
的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标)
(2)求代数式  的最小值
的最小值
阅读材料:(本题8分)
例:说明代数式  的几何意义,并求它的最小值.
的几何意义,并求它的最小值.
解:  ,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则
,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则 可以看成点P与点A(0,1)的距离,
可以看成点P与点A(0,1)的距离, 可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,
只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,
所以PA′+PB的最小值为线段A′B的长度.为此,构造直角
三角形A′CB,因为A′C=3,CB=3,所以A′B= ,
,
即原式的最小值为 。
。
根据以上阅读材料,解答下列问题:
(1)代数式 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标)
的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标)
(2)求代数式  的最小值
的最小值

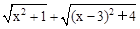 的几何意义,并求它的最小值.
的几何意义,并求它的最小值.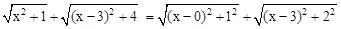 ,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则
,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则 可以看成点P与点A(0,1)的距离,
可以看成点P与点A(0,1)的距离, 可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值. ,
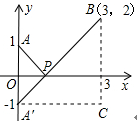
, 。
。
 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标)
的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标) 的最小值
的最小值对于多项式![]() ,如果我们把
,如果我们把![]() 代入此多项式,发现多项式
代入此多项式,发现多项式![]() =0,这时可以断定多项式中有因式
=0,这时可以断定多项式中有因式![]() (注:把
(注:把![]() 代入多项式能使多项式的值为0,则多项式含有因式
代入多项式能使多项式的值为0,则多项式含有因式![]() ),于是我们可以把多项式写成:
),于是我们可以把多项式写成: ![]() =
=![]() ,(1)求式子中
,(1)求式子中![]() 、
、![]() 的值;(2)以上这种因式分解的方法叫试根法,用试根法分解多项式
的值;(2)以上这种因式分解的方法叫试根法,用试根法分解多项式![]() 的因式。
的因式。

 H2(g)+CO2(g),该反应的化学平衡常数表达式为K= ;反应的平衡常数随温度的变化如表一,
H2(g)+CO2(g),该反应的化学平衡常数表达式为K= ;反应的平衡常数随温度的变化如表一,| 温度/℃ | 400 | 500 | 830 | 1000 |
| 平衡常数K | 10 | 9 | 1 | 0.6 |
 H2(g)+CO2(g),在830℃,以表二的物质的量(单位为mol)投入恒容反应器发生上述反应,其中反应开始时,向正反应方向进行的有 (填实验编号);
H2(g)+CO2(g),在830℃,以表二的物质的量(单位为mol)投入恒容反应器发生上述反应,其中反应开始时,向正反应方向进行的有 (填实验编号);| 实验编号 | N(CO) | N(H2O) | n(H2) | N(CO2) |
| A | 1 | 5 | 2 | 3 |
| B | 2 | 2 | 1 | 1 |
| C | 0.5 | 2 | 1 | 1 |
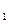 达到平衡、在时刻t
达到平衡、在时刻t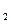 分别因改变某个条件而发生变化的情况:图中时刻t
分别因改变某个条件而发生变化的情况:图中时刻t 发生改变的条件是_________。(写出两种)
发生改变的条件是_________。(写出两种)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com