
题目列表(包括答案和解析)
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆周上的一点.
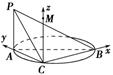
(1)求证:平面PAC⊥平面PBC;(6分)
(2)若AB=2,AC=1,PA=1,求二面角CPBA的余弦值.(6分)
(本小题满分13分)已知函数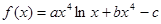 (x>0)在x = 1处取得极值–3–c,其中a,b,c为常数。
(x>0)在x = 1处取得极值–3–c,其中a,b,c为常数。
(1)试确定a,b的值;(6分)
(2)讨论函数f(x)的单调区间;(4分)
(3)若对任意x>0,不等式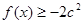 恒成立,求c的取值范围。(3分)
恒成立,求c的取值范围。(3分)
(12分)如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD//BC且AD﹥BC,∠DAB=∠ABC=90°,PA=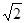 ,AB=BC=1。M为PC的中点。
,AB=BC=1。M为PC的中点。
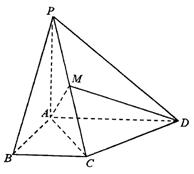
(1)求二面角M—AD—C的大小;(6分)
(2)如果∠AMD=90°,求线段AD的长。(6分)
已知椭圆C: 的两个焦点为F1、F2,点P在椭圆C上,且|PF1|=
的两个焦点为F1、F2,点P在椭圆C上,且|PF1|= ,
,
|PF2|= , PF1⊥F1F2.
, PF1⊥F1F2.
(1)求椭圆C的方程;(6分)
(2)若直线L过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程.
在边长为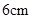 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
(I)判别MN与平面AEF的位置关系,并给出证明;
(II)求多面体E-AFMN的体积.


【解析】第一问因翻折后B、C、D重合(如下图),所以MN应是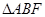 的一条中位线,则利用线线平行得到线面平行。
的一条中位线,则利用线线平行得到线面平行。
第二问因为 平面BEF,……………8分
平面BEF,……………8分
且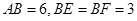 ,
,
∴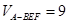 ,又
,又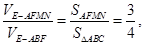 ∴
∴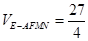
(1)因翻折后B、C、D重合(如图),

所以MN应是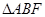 的一条中位线,………………3分
的一条中位线,………………3分
则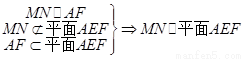 .………6分
.………6分
(2)因为 平面BEF,……………8分
平面BEF,……………8分
且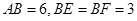 ,
,
∴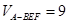 ,………………………………………10分
,………………………………………10分
又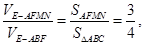 ∴
∴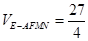
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com