
题目列表(包括答案和解析)
用向量方法证明顺次连结任一四边形各边中点所得的四边形为平行四边形.
证明顺次连结A(-4,3),B(2,5),C(6,3)和D(-3,0)所成的四边形是直角梯形,并求出此梯形的面积.
 选修4-1:几何证明选讲
选修4-1:几何证明选讲| x2 |
| 4 |
| y2 |
| 3 |
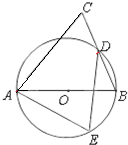 选修4-1几何证明
选修4-1几何证明湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com