(13分)如图所示，A为一具有光滑曲面的固定轨道，轨道底端是水平的，质量的小车B静止于轨道右侧，其板面与轨道底端靠近且在同一水平面上，小车板面足够长，一个质量的物体以的初速度从轨道顶端滑下，冲上小车B后经一段时间与小车相对静止并一起继续运动，若轨道顶端与底端水平面的高度差为，物体与小车板面间的动摩擦因数为，小车与水平面间的摩擦忽略不计(取)，求：

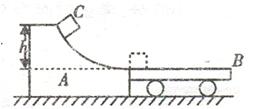
(1)物体与小车保持相对静止时的速度；

(2)从物体冲上小车到与小车相对静止所用的时间；          

[物理――选修3-5]（27分）
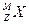（1） (5分)放射性元素的原子核连续经过三次α衰变和两次β衰变．若最后变成另一种元素的原子核Y，则新核Y的正确写法是

A．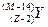

B．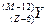

C．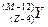

D．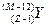

[物理――选修3-5]（27分）

（1） (5分)放射性元素的原子核连续经过三次α衰变和两次β衰变．若最后变成另一种元素的原子核Y，则新核Y的正确写法是

A．        B．     C．        D．

（2） (6分) 现有一群处于n=4能级上的氢原子，已知氢原子的基态能量E₁=－13.6 eV，氢原子处于基态时电子绕核运动的轨道半径为r，静电力常量为k，普朗克常量h=6.63×10^－34 J·s.则电子在n=4的轨道上运动的动能是    J；这群氢原子发出的光子的最大频率是      Hz。

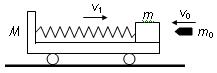
（3）(16分)如图所示，光滑水平面上有一辆质量为M＝1 kg的小车，小车的上表面有一个质量为m＝0.9 kg的滑块，在滑块与小车的挡板间用轻弹簧相连接，滑块与小车上表面间的动摩擦因数为μ＝0.2，整个系统一起以v₁＝10 m/s的速度向右做匀速直线运动．此时弹簧长度恰好为原长．现在用质量为m₀＝0.1 kg的子弹，以v₀＝50 m/s的速度向左射入滑块且不穿出，所用时间极短．已知当弹簧压缩到最短时的弹性势能为E_p＝8.6 J．（g取10m/s²）求：

（ⅰ）子弹射入滑块的瞬间滑块的速度；

（ⅱ）从子弹射入到弹簧压缩最短，滑块在车上滑行的距离．

[物理――选修3-5]（27分）

（1） (5分)放射性元素的原子核连续经过三次α衰变和两次β衰变．若最后变成另一种元素的原子核Y，则新核Y的正确写法是

A．         B．     C．         D．

（2） (6分) 现有一群处于n=4能级上的氢原子，已知氢原子的基态能量E₁=－13.6 eV，氢原子处于基态时电子绕核运动的轨道半径为r，静电力常量为k，普朗克常量h=6.63×10^－34 J·s.则电子在n=4的轨道上运动的动能是     J；这群氢原子发出的光子的最大频率是      Hz。

（3）(16分)如图所示，光滑水平面上有一辆质量为M＝1 kg的小车，小车的上表面有一个质量为m＝0.9 kg的滑块，在滑块与小车的挡板间用轻弹簧相连接，滑块与小车上表面间的动摩擦因数为μ＝0.2，整个系统一起以v₁＝10 m/s的速度向右做匀速直线运动．此时弹簧长度恰好为原长．现在用质量为m₀＝0.1 kg的子弹，以v₀＝50 m/s的速度向左射入滑块且不穿出，所用时间极短．已知当弹簧压缩到最短时的弹性势能为E_p＝8.6 J．（g取10m/s²）求：

（ⅰ）子弹射入滑块的瞬间滑块的速度；

（ⅱ）从子弹射入到弹簧压缩最短，滑块在车上滑行的距离．