已知函数的定义域为。

（1）求证：直线（其中）不是函数图像的切线；

（2）判断在上单调性，并证明；

（3）已知常数满足，求关于的不等式的解集

已知函数的定义域为，且同时满足下列条件：（1）是奇函数；

（2）在定义域上单调递减；（3）求的取值范围。

（12分）已知函数的定义域为，且同时满足下列条件：（1）是奇函数；（2）在定义域上单调递减；（3）求的取值范围 

已知函数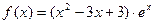的定义域为[－2，t](t>－2)，
（Ⅰ）试确定t的取值范围，使得函数在[－2，t]上为单调函数；
（Ⅱ）求证：对于任意的t>－2，总存在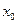∈(－2，t)，满足，
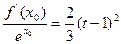并确定这样的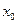的个数.

已知函数的定义域为，值域为.下列关于函数的说法：①当时，；②将的图像补上点，得到的图像必定是一条连续的曲线；③是上的单调函数；④的图象与坐标轴只有一个交点.其中正确命题的个数为（  ）

A. 1                  B. 2              C. 3               D. 4