已知动点p(x,y),满足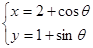,,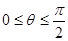则动点p所表示的曲线长度为        

 

已知动点P(x,y)在椭圆=1上,若A点坐标为(3,0),||=1且·=0，则||的最小值是___________.

(理)设关于x的方程x²-mx-1=0有两个实根α、β,且α＜β.定义函数f(x)=.

(1)求αf(α)+βf(β)的值;

(2)判断f(x)在区间(α,β)上的单调性,并加以证明;

(3)若λ、μ为正实数,证明不等式:|f()-f()|＜|α-β|.

(文)如图,在平面直角坐标系中,已知动点P(x,y),PM⊥y轴,垂足为M,点N与点P关于x轴对称,且=4.

(1)求动点P的轨迹W的方程;

(2)若点Q的坐标为(2,0),A、B为W上的两个动点,且满足QA⊥QB,点Q到直线AB的距离为d,求d的最大值.