
题目列表(包括答案和解析)
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数 学 | 1.3 | 12.3 | 25.7 | 36.7 | 50.3 | 67.7 | 49.0 | 52.0 | 40.0 | 34.3 |
| 物 理 | 2.3 | 9.7 | 31.0 | 22.3 | 40.0 | 58.0 | 39.0 | 60.7 | 63.3 | 42.7 |
| 学生序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数 学 | 78.3 | 50.0 | 65.7 | 66.3 | 68.0 | 95.0 | 90.7 | 87.7 | 103.7 | 86.7 |
| 物 理 | 49.7 | 46.7 | 83.3 | 59.7 | 50.0 | 101.3 | 76.7 | 86.0 | 99.7 | 99.0 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数 学 | 1.3 | 12.3 | 25.7 | 36.7 | 50.3 | 67.7 | 49.0 | 52.0 | 40.0 | 34.3 |
| 物 理 | 2.3 | 9.7 | 31.0 | 22.3 | 40.0 | 58.0 | 39.0 | 60.7 | 63.3 | 42.7 |
| 学生序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数 学 | 78.3 | 50.0 | 65.7 | 66.3 | 68.0 | 95.0 | 90.7 | 87.7 | 103.7 | 86.7 |
| 物 理 | 49.7 | 46.7 | 83.3 | 59.7 | 50.0 | 101.3 | 76.7 | 86.0 | 99.7 | 99.0 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
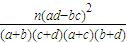 ,其中n=a+b+c+d)
,其中n=a+b+c+d)| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数 学 | 1.3 | 12.3 | 25.7 | 36.7 | 50.3 | 67.7 | 49.0 | 52.0 | 40.0 | 34.3 |
| 物 理 | 2.3 | 9.7 | 31.0 | 22.3 | 40.0 | 58.0 | 39.0 | 60.7 | 63.3 | 42.7 |
| 学生序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数 学 | 78.3 | 50.0 | 65.7 | 66.3 | 68.0 | 95.0 | 90.7 | 87.7 | 103.7 | 86.7 |
| 物 理 | 49.7 | 46.7 | 83.3 | 59.7 | 50.0 | 101.3 | 76.7 | 86.0 | 99.7 | 99.0 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
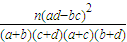 ,其中n=a+b+c+d)
,其中n=a+b+c+d)| 组号 | 分组 | 频数 | 频率 |
| 1 | [0,20) | 162 | 0.81 |
| 2 | [20,40) | 18 | 0.09 |
| 3 | [40,60) | 10 | y |
| 4 | [60,80) | 6 | 0.03 |
| 5 | [80,100) | x | 0.02 |
| 组号 | 分组 | 频数 | 频率 |
| 1 | [0,20) | 162 | 0.81 |
| 2 | [20,40) | 18 | 0.09 |
| 3 | [40,60) | 10 | y |
| 4 | [60,80) | 6 | 0.03 |
| 5 | [80,100) | x | 0.02 |
一、选择题:(本大题共8小题,每小题5分,共40分.)
题号
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
答案
A
B
A
D
D
B
C
C
二、填空题(本大题共6小题,每小题5分,有两空的小题,第一空3分,第二空2分,共30分)
(9) (10)(2,-1) (11)
(10)(2,-1) (11) ,或
,或 (12)
(12) (13)(0,1),(x-1)2+(y-3)2=1
(13)(0,1),(x-1)2+(y-3)2=1
(14)10,4n-2
三、解答题(本大题共6小题,共80分.)
(15)(共12分)
解:(Ⅰ)∵p = (sinx,cosx+sinx),q=(2cosx,cosx-sinx),
∴f(x) = p?q=(sinx,cosx+sinx)?(2cosx,cosx-sinx)
=2sinxcosx+cos2x-sin2x………………………………………………2分
=sin2x+cos2x……………………………………………………………4分
∴f( ) =
) = …………………………………………………………………5分
…………………………………………………………………5分
又f(x) = sin2x+cos2x = ………………………………………6分
………………………………………6分
∴函数f(x)的最大值为 . ……………………………………………………7分
. ……………………………………………………7分
当且仅当x= +k
+k (k
(k Z)时,函数f(x)取得最大值
Z)时,函数f(x)取得最大值 .
.
(Ⅱ)由2 -
- ≤2x+
≤2x+ ≤2
≤2 +
+ (k
(k Z) …………………………………9分
Z) …………………………………9分
得 -
- ≤x≤
≤x≤ +
+ (k
(k Z), …………………………………………11分
Z), …………………………………………11分
∴函数f(x)的单调递增区间为[ -
- ,
, +
+ ] (k∈Z). …………12分
] (k∈Z). …………12分
(16)(共14分)
解法一:
解:(Ⅰ)∵SA⊥AB,SA⊥AC,且AB∩AC=A. ∴SA⊥平面ABC.…………………………2分
∴AC为SC在平面ABC内的射影. ……………………………………………3分
又AC⊥BC,∴BC⊥SC……………………………………………………………………4分
(Ⅱ)由(Ⅰ)BC⊥SC,又BC⊥AC,
∴∠SCA为所求二面角的平面角…………………………………………………………6分
又∵SB=4 ,BC=4,
,BC=4,
∴SC=4. ∵AC=2,∴∠SCA=60°…………………………………………………9分
即二面角A-BC-S的大小为60°
 (Ⅲ)过A作AD⊥SC于D,连结BD,
(Ⅲ)过A作AD⊥SC于D,连结BD,
由(Ⅱ)得BC⊥平面SAC,
又BC 平面SBC,
平面SBC,
∴平面SAC⊥平面SBC,
且平面SAC 平面SBC=SC.
平面SBC=SC.
∴AD⊥平面SBC.
∴BD为AB在平面SBC内的射影.
∴∠ABD为AB与平面SBC所成角.…………………………11分
在Rt△ABC中,AB= ,
,
在Rt△SAC中,SA= =2
=2 ,
,
AD= .
.
∴sinABD= .……………………………………………………………………13分
.……………………………………………………………………13分
所以直线AB与平面SBC所成角的大小为arcsin .…………………………………14分
.…………………………………14分
解法二:
解:(Ⅰ)由已知∠SAB=∠SAC=∠ACB=90°,
以C点为原点,建立如图所示的空间直角坐标系C - xyz.
 则A(0,2,0),B(4,0,0),C(0,0,0),S(0,2,
则A(0,2,0),B(4,0,0),C(0,0,0),S(0,2, ).……………………………2分
).……………………………2分
则 =(0,- 2,
=(0,- 2, ),
),
 =(-4,0,0).
=(-4,0,0).
∴ ?
? =0.
=0.
∴SC⊥BC.…………………………………………………………4分(Ⅱ)∵∠SAB=∠SAC=90°,
∴SA⊥平面ABC.
∴ =(0,0,
=(0,0, )是平面ABC的法
)是平面ABC的法
向量.…………………………………………………………………5分
设侧面SBC的法向量为
n=(x,y,z),
 =(0,- 2,-
=(0,- 2,- ),
), =(-4,0,0).
=(-4,0,0).
∵ ?n=0,
?n=0, ?n=0,
?n=0,
∴ ∴x=0.令z=1则y=
∴x=0.令z=1则y= ,
,
则平面SBC的一个法向量n=(0, ,1).……………………………………………7分
,1).……………………………………………7分
 cos
cos
 ,n
,n = =
= = .……………………………………………………8分
.……………………………………………………8分
即二面角A-BC-S的大小为60°.……………………………………………………9分
(Ⅲ)由(Ⅱ)可知n=(0,- ,1)是平面SBC的一个法向量.……………………………10分
,1)是平面SBC的一个法向量.……………………………10分
又 =(4,-2,0),
=(4,-2,0),
 ∴cos
∴cos
 ,n
,n =
=
=
= .…………………………………………13分
.…………………………………………13分
所以直线AB与平面SBC所成角为arcsin .…………………………………………14分
.…………………………………………14分
(17)(共13分)
解:(Ⅰ)设乙闯关成功的概率为P1,丙闯关成功的概率为P2………………………1分
因为乙丙独立闯关,根据独立事件同时发生的概率公式得:
 ………………………………………………………………………3分
………………………………………………………………………3分
解得P1= ,P2=
,P2= .…………………………………………………………5分
.…………………………………………………………5分
答:乙闯关成功的概率为 ,丙闯关成功的概率为
,丙闯关成功的概率为 .
.
(Ⅱ)团体总分为4分,即甲、乙、丙三人中恰有2人过关,而另外一个没过关.
设“团体总分为4分”为事件A,………………………………………………6分
则P(A)=(1- )
)
 .
.
………………………………………………………………………………………9分
答:团体总分为4分的概率为 .
.
(Ⅲ)团体总分不小于4分,即团体总分为4分或6分,
设“团体总分不小于4分”为事件B,…………………………………………10分
由(Ⅱ)知团体总分为4分的概率为 .
.
团体总分为6分,即3人都闯关成功的概率为 ………………12分
………………12分
所以参加复赛的概率为P(B)= .…………………………………13分
.…………………………………13分
答:该小组参加复赛的概率为 .
.
(18)(共13分)
解:(Ⅰ)第5行第5个数是29.……………………………………………………………2分
(Ⅱ)由f(1)=n2,得a1+a2+a3+…+an=n2.…………………………………………………3分
设Sn是数列{an}的前n项和,∴Sn=n2.……
当n=1时,a1=S1=1,…………………………………………………………………5分
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1.………………………………………6分
又当n=1时,2n-1=1=a1,
∴an=2n-1. ………………………………………………………………………8分
即数列{an}的通项公式是an=2n-1(n=1,2,3,…).
(Ⅲ)由(Ⅱ)知数列{an}是首项为1,公差为2的等差数列.……………………………9分
∵前m-1行共有项1+2+3+…+(m-1)=  ,
,
∴第m行的第一项为 =2×
=2× -1=m2-m+1.………………11分
-1=m2-m+1.………………11分
∴第m行构成首项为m2-m+1,公差为2的等差数列,且有m项.
∴Tm=(m2-m+1)×m+ ×2=m3.……………………………………13分
×2=m3.……………………………………13分
(19)(共14分)
解:(Ⅰ)设Q(x,y),由已知得点Q在FP的中垂线上,……………………………1分
即|QP|=|QF|. ……………………………………………………………………2分
根据抛物线的定义知点Q在以F为焦点,直线m为准线的抛 物线上,…4分
所以点Q的轨迹方程为y2=4x(x≠0). …………………………………………6分
(注:没有写出x≠0扣1分)
(Ⅱ)当直线l的斜率不存在时,点A坐标为(2, ),点B坐标为(2,-
),点B坐标为(2,- ),
),
∵点F坐标为(1,0),可以推出∠AFB≠ …………………………………8分
…………………………………8分
当直线l的斜率存在时,
设l的方程为y=k(x-2),它与抛物线y2=4x的交点坐标分别为A(x1,y1),
B(x2,y2)
由
 得x1x2=4,y1y2=-8.……………………………………10分
得x1x2=4,y1y2=-8.……………………………………10分
假定θ= ,则有cosθ=
,则有cosθ= ,
,
如图,即 ,
(*)
,
(*)
由定义得|AF|=x1+1,|BF|=x2+1.
从而有|AF|2+|BF|2-|AB|2
=(x1+1)2+(x2+1)2-(x1-x2)2-(y1-y2)2
=-2(x1+x2)-6
∴|AF|?|BF|=(x1+1)(x2+1)=x1x2+x1+x2+1=x1+x2+5.…………………………12分
将上式代入(*)得 ,即x1+x2+1=0.
,即x1+x2+1=0.
这与x1>0且x2>0相矛盾.
综上,θ不能等于 .…………………………………………………………14分
.…………………………………………………………14分
(20)(共14分)
解:(Ⅰ) =-3x2+2ax.………………………………………………………………1分
=-3x2+2ax.………………………………………………………………1分
据题意, =tan
=tan =1, ∴-3+2a=1,即a=2.……………………………3分
=1, ∴-3+2a=1,即a=2.……………………………3分
(Ⅱ)由(Ⅰ)知f(x)= x3+2x2
x3+2x2 4,
4,
则f′(x)= 3x2+4x.
3x2+4x.
x
 1
1
( 1,0)
1,0)
0
(0,1)
1
f′(x)
 7
7

0
+
1
f(x)
 1
1

 4
4

 3
3
…………………………………………………………………………………5分
∴对于m [
[ 1,1],f(m)的最小值为f(0)=
1,1],f(m)的最小值为f(0)= 4……………………………6分
4……………………………6分
∵f′(x)= 3x2+4x的对称轴为x=
3x2+4x的对称轴为x= ,且抛物线开口向下,
,且抛物线开口向下,
∴x [
[ 1,1]时,f′(x)最小值为f′(
1,1]时,f′(x)最小值为f′( 1)与f′(1)中较小的.
1)与f′(1)中较小的.
∵f′(1)=1, f′( 1)=
1)= 7,
7,
∴当x [
[ 1,1]时,f′(x)最小值为
1,1]时,f′(x)最小值为 7.
7.
∴当n [
[ 1,1]时,f′(n)最小值为
1,1]时,f′(n)最小值为 7.……………………………………7分∴f(m)+ f′(n)的最小值为
7.……………………………………7分∴f(m)+ f′(n)的最小值为 11.……………………………………………8分(Ⅲ)∵f′(x)=
11.……………………………………………8分(Ⅲ)∵f′(x)= 3x(x
3x(x
 ).
).
①若a≤0,当x>0时,f′(x)<0, ∴f(x)在[0,+∞]上单调递减.
又f(0)= 4,则当x>0时, f(x)<
4,则当x>0时, f(x)< 4.
4.
∴当a≤0时,不存在x0>0,使f(x0)>0.…………………………………11分
②若a>0,则当0<x< 时,f′(x)>0,当x>
时,f′(x)>0,当x> 时,f′(x)<0.
时,f′(x)<0.
从而f(x)在(0,  ]上单调递增,在[
]上单调递增,在[ ,+∞)上单调递减.
,+∞)上单调递减.
∴当x (0,+∞)时,f(x)max=f(
(0,+∞)时,f(x)max=f( )=
)=
 +
+
 4=
4=
 4.
4.
据题意,
 4>0,即a3>27. ∴a>3. …………………………………14分
4>0,即a3>27. ∴a>3. …………………………………14分
综上,a的取值范围是(3,+∞).
说明:其他正确解法按相应步骤给分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com