
题目列表(包括答案和解析)
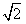 a,
a,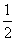 AB;②AB=
AB;②AB=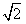 a;③CM⊥AB;④BC⊥AC。请你从中再选择两个条件以确定cosθ的值,并求解.
a;③CM⊥AB;④BC⊥AC。请你从中再选择两个条件以确定cosθ的值,并求解. 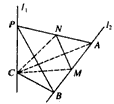
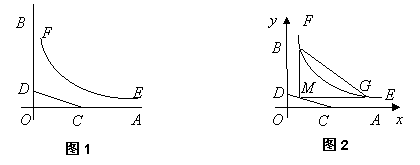
如图1,![]() ,
,![]() 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段![]() 和曲线段
和曲线段![]() 分别是湖泊中的一座栈桥和一条防波堤。为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤。为观光旅游的需要,拟过栈桥![]() 上某点
上某点![]() 分别修建与
分别修建与![]() ,
,![]() 平行的栈桥
平行的栈桥![]() 、
、![]() ,且以
,且以![]() 、
、![]() 为边建一个跨越水面的三角形观光平台
为边建一个跨越水面的三角形观光平台![]() 。建立如图2所示的直角坐标系,测得线段
。建立如图2所示的直角坐标系,测得线段![]() 的方程是
的方程是![]() ,曲线段
,曲线段![]() 的方程是
的方程是![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,记
,记![]() 。(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
。(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
(1)求![]() 的取值范围;
的取值范围;
(2)试写出三角形观光平台![]() 面积
面积![]() 关于
关于![]() 的函数解析式,并求出该面积的最小值。
的函数解析式,并求出该面积的最小值。

如图,已知圆锥体 的侧面积为
的侧面积为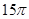 ,底面半径
,底面半径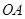 和
和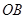 互相垂直,且
互相垂直,且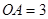 ,
, 是母线
是母线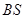 的中点.
的中点.

(1)求圆锥体的体积;
(2)异面直线 与
与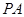 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
【解析】本试题主要考查了圆锥的体积和异面直线的所成的角的大小的求解。
第一问中,由题意, 得
得 ,故
,故
从而体积 .2中取OB中点H,联结PH,AH.
.2中取OB中点H,联结PH,AH.
由P是SB的中点知PH//SO,则 (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.在
AH.在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
则 ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan
解:(1)由题意, 得
得 ,
,
故 从而体积
从而体积 .
.
(2)如图2,取OB中点H,联结PH,AH.
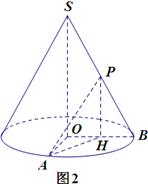
由P是SB的中点知PH//SO,则 (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.
AH.
在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
则 ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan
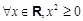 ”的否定是“
”的否定是“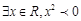 ”;
”;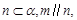 则
则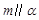 ;
;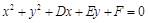 与坐标轴4个交点,分别为
与坐标轴4个交点,分别为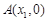 ,
,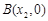 ,
,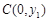 ,
,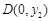 ,则
,则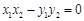 ;
;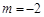 ”是“直线
”是“直线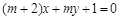 与直线
与直线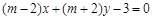 相互垂直”的必要不充分条件。
相互垂直”的必要不充分条件。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com