(18分)如图所示，在光滑绝缘的水平面内，对角线AC将边长为L的正方形分成ABC和ADC两个区域，ABC区域有垂直于水平面的匀强磁场，ADC区域有平行于DC并由C指向D的匀强电场。质量为m、带电量为+q的粒子从A点沿AB方向以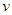的速度射入磁场区域，从对角线AC的中点进入电场区域。

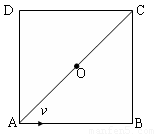
（1）判断磁场的方向并求出磁感强度B的大小。

（2）讨论电场强度E在不同取值时，带电粒子在电场中运动的时间t。

(18分)

为了使粒子经过一系列的运动后，又以原来的速率沿相反方向回到原位，可设计如下的一个电磁场区域（如图所示）：水平线QC以下是水平向左的匀强电场，区域Ⅰ(梯形PQCD)内有垂直纸面向里的匀强磁场，磁感应强度为B；区域Ⅱ(三角形APD)内的磁场方向与Ⅰ内相同，但是大小可以不同，区域Ⅲ(虚线PD之上、三角形APD以外)的磁场与Ⅱ内大小相等、方向相反。已知等边三角形AQC的边长为2l，P、D分别为AQ、AC的中点。带正电的粒子从Q点正下方、距离Q点为l的O点以某一速度射出，在电场力作用下从QC边中点N以速度v₀垂直QC射入区域Ⅰ，再从P点垂直AQ射入区域Ⅲ，又经历一系列运动后返回O点。（粒子重力忽略不计）求：

（1）该粒子的比荷；

（2）粒子从O点出发再回到O点的整个运动过程所需时间。

(18分)

    为了使粒子经过一系列的运动后，又以原来的速率沿相反方向回到原位，可设计如下的一个电磁场区域(如图所示)：水平线QC以下是水平向左的匀强电场，区域I(梯形PQCD)

内有垂直纸面向里的匀强磁场，磁感应强度为B；区域II(三角形APD)内的磁场方向与I内相同，但是大小可以不同，区域Ⅲ(虚线PD之上、三角形APD以外)的磁场与Ⅱ内大小相等、方向相反。已知等边三角形AQC的边长为2L，P、D分别为AQ、AC的中点。带正电的粒子从Q点正下方、距离Q点为L的0点以某一速度射出：在电场力作用下从QC边中点N，以速度V₀垂直QC射入区域Ⅰ，再从P点垂直AQ射入区域Ⅲ，又经历一系列运动后返回O点。(粒子重力忽略不计)求：

    (1)该粒子的比荷；

(2)粒子从O点出发再回到O点的整个运动过程所需时间。

(10分)如图所示，质量分布不均匀的直细杆AB长1 m，将它的两端用两根细绳拴住吊在两竖直墙上，当AB在水平方向平衡时，细绳AC与竖直方向的夹角为θ₁＝60°，细绳BD与竖直方向的夹角为θ₂＝30°.求AB杆的重心距B端的距离．

图4－18

【解析】：以AB杆为研究对象，受力分析如图所示，AC绳的拉力为F₁，BD绳的拉力为F₂.F₁、F₂的作用线交于E点，则重力G的作用线必过E点．过E点作竖直线交AB杆于O点，O点即为AB杆重心的位置．

[来源:学§科§网]

由几何关系可知

＝·sin30°＝·sin30°·sin30°

＝＝0.25 m.

即细杆的重心距B端0.25 m.

(10分)如图所示，质量分布不均匀的直细杆AB长1 m，将它的两端用两根细绳拴住吊在两竖直墙上，当AB在水平方向平衡时，细绳AC与竖直方向的夹角为θ₁＝60°，细绳BD与竖直方向的夹角为θ₂＝30°.求AB杆的重心距B端的距离．

图4－18

【解析】：以AB杆为研究对象，受力分析如图所示，AC绳的拉力为F₁，BD绳的拉力为F₂.F₁、F₂的作用线交于E点，则重力G的作用线必过E点．过E点作竖直线交AB杆于O点，O点即为AB杆重心的位置．

由几何关系可知

＝·sin30°＝·sin30°·sin30°

＝＝0.25 m.

即细杆的重心距B端0.25 m.