
题目列表(包括答案和解析)
| 1 |
| 2 |
| v | 2 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| v | 2 1 |
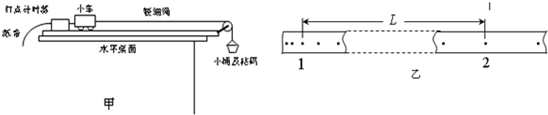
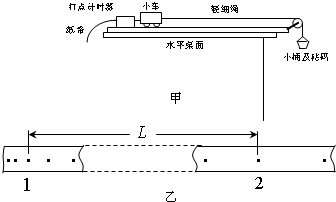
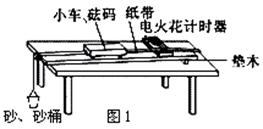
图1为验证牛顿第二定律的实验装置示意图.图中打点计时器的电源为50Hz的交流电源,打点的时间间隔用Δt表示.在小车质量M未知的情况下,某同学设计了一种方法用来研究“在外力一定的条件下,物体的加速度与其质量间的关系”.

(1)完成下列实验步骤中的填空:
①平衡小车所受的阻力:撤去砂和砂桶,调整木板右端的高度,用手轻拨小车,直到打点计时器打出一系列 的点.
②按住小车,在左端挂上适当质量的砂和砂桶,在小车中放入砝码.
③打开打点计时器电源,释放小车,获得带有点迹的纸带,在纸带上标出小车中砝码的质量m.
④按住小车,改变小车中砝码的质量,重复步骤③.
⑤在每条纸带上清晰的部分,每5个间隔标注一个计数点.测量相邻计数点的间距s1,s2,….求出与不同m相对应的加速度a.
⑥以砝码的质量m为横坐标, 为纵坐标,在坐标纸上做出
为纵坐标,在坐标纸上做出 -m关系图线.若加速度与小车和砝码的总质量成反比,则
-m关系图线.若加速度与小车和砝码的总质量成反比,则 与m应成 关系(填“线性”或“非线性”).
与m应成 关系(填“线性”或“非线性”).
(2)完成下列填空:
①本实验中,为了保证在改变小车中砝码的质量时,小车所受的拉力近似不变,悬挂砂和砂桶的总质量应满足的条件是 .
②如图2所示是该同学在某次实验中利用打点计时器打出的一条纸带,A、B、C、D是该同学在纸带上选取的连续四个计数点.该同学用刻度尺测出AC间的距离为SⅠ,测出BD间的距离为SⅡ.a可用SⅠ、SⅡ和Δt(打点的时间间隔)表示为a= .


③图3为所得实验图线的示意图.设图中直线的斜率为k,在纵轴上的截距为b,若牛顿定律成立,则小车受到的拉力为 ,小车的质量为 .
图1为验证牛顿第二定律的实验装置示意图.图中打点计时器的电源为50Hz的交流电源,打点的时间间隔用Δt表示.在小车质量M未知的情况下,某同学设计了一种方法用来研究“在外力一定的条件下,物体的加速度与其质量间的关系”.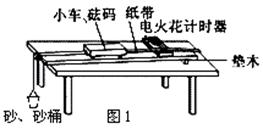
(1)完成下列实验步骤中的填空:
①平衡小车所受的阻力:撤去砂和砂桶,调整木板右端的高度,用手轻拨小车,直到打点计时器打出一系列 的点.
②按住小车,在左端挂上适当质量的砂和砂桶,在小车中放入砝码.
③打开打点计时器电源,释放小车,获得带有点迹的纸带,在纸带上标出小车中砝码的质量m.
④按住小车,改变小车中砝码的质量,重复步骤③.
⑤在每条纸带上清晰的部分,每5个间隔标注一个计数点.测量相邻计数点的间距s1,s2,….求出与不同m相对应的加速度a.
⑥以砝码的质量m为横坐标,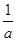 为纵坐标,在坐标纸上做出
为纵坐标,在坐标纸上做出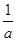 -m关系图线.若加速度与小车和砝码的总质量成反比,则
-m关系图线.若加速度与小车和砝码的总质量成反比,则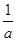 与m应成 关系(填“线性”或“非线性”).
与m应成 关系(填“线性”或“非线性”).
(2)完成下列填空:
①本实验中,为了保证在改变小车中砝码的质量时,小车所受的拉力近似不变,悬挂砂和砂桶的总质量应满足的条件是 .
②如图2所示是该同学在某次实验中利用打点计时器打出的一条纸带,A、B、C、D是该同学在纸带上选取的连续四个计数点.该同学用刻度尺测出AC间的距离为SⅠ,测出BD间的距离为SⅡ.a可用SⅠ、SⅡ和Δt(打点的时间间隔)表示为a= .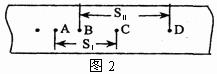
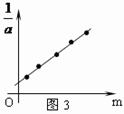
③图3为所得实验图线的示意图.设图中直线的斜率为k,在纵轴上的截距为b,若牛顿定律成立,则小车受到的拉力为 ,小车的质量为 .
图1为验证牛顿第二定律的实验装置示意图.图中打点计时器的电源为50Hz的交流电源,打点的时间间隔用Δt表示.在小车质量M未知的情况下,某同学设计了一种方法用来研究“在外力一定的条件下,物体的加速度与其质量间的关系”.
(1)完成下列实验步骤中的填空:
①平衡小车所受的阻力:撤去砂和砂桶,调整木板右端的高度,用手轻拨小车,直到打点计时器打出一系列 ▲ 的点.
②按住小车,在左端挂上适当质量的砂和砂桶,在小车中放入砝码.
③打开打点计时器电源,释放小车,获得带有点迹的纸带,在纸带上标出小车中砝码的质量m.
④按住小车,改变小车中砝码的质量,重复步骤③.
⑤在每条纸带上清晰的部分,每5个间隔标注一个计数点.测量相邻计数点的间距s1,s2,….求出与不同m相对应的加速度a.
⑥以砝码的质量m为横坐标,![]() 为纵坐标,在坐标纸上做出
为纵坐标,在坐标纸上做出![]() -m关系图线.若加速度与小车和砝码的总质量成反比,则
-m关系图线.若加速度与小车和砝码的总质量成反比,则![]() 与m应成 ▲ 关系(填“线性”或“非线性”).
与m应成 ▲ 关系(填“线性”或“非线性”).
(2)完成下列填空:
①本实验中,为了保证在改变小车中砝码的质量时,小车所受的拉力近似不变,悬挂砂和砂桶的总质量应满足的条件是 ▲ .
②如图2所示是该同学在某次实验中利用打点计时器打出的一条纸带,A、B、C、D是该同学在纸带上选取的连续四个计数点.该同学用刻度尺测出AC间的距离为SⅠ,测出BD间的距离为SⅡ.a可用SⅠ、SⅡ和Δt(打点的时间间隔)表示为a= ▲ .
③图3为所得实验图线的示意图.设图中直线的斜率为k,在纵轴上的截距为b,若牛顿定律成立,则小车受到的拉力为 ▲ ,小车的质量为 ▲ .


一、1、C 2、B3、AB 4、BCD5、AD 6、A 7、AD 8、B
二、实验题:(18分)将答案填在题目的空白处,或者要画图连线。
9、(6分)①小桶和砝码的总重力理科综合.files/image085.gif) 大于轻细绳的拉力
大于轻细绳的拉力理科综合.files/image087.gif) ,即
,即理科综合.files/image058.gif) 偏大(3分)
偏大(3分)
②ACD (3分)
10、(12分)(1 )A1 (3分) (2)R1 (3分)(3)电路图如图所示(6分)
理科综合.files/image090.jpg)
三、本大题共三小题共计54分.解答时请写出必要的文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分.有数值计算的题.答案中必须明确写出数值和单位
11、(16分)(1)理科综合.files/image094.gif)
甲运动到C点时,乙的速度为零
理科综合.files/image098.gif)
理科综合.files/image102.gif) (5分)
(5分)
(2)当连接甲球的细线与圆环相切时,甲、乙速度相等,此时甲球到达A'点,离开桌面的距离为d
理科综合.files/image106.gif)
理科综合.files/image110.gif) (5分)
(5分)
(3)由机械能守恒可得 理科综合.files/image114.gif)
理科综合.files/image118.gif)
理科综合.files/image120.gif) (6分)
(6分)
12、(18分)(1)金属棒cd从静止开始运动直至细绳刚好被拉断的过程中有:
Qab =U2t/Rab ① (1分) QR=U2t/R ② (1分)
联立①②可得Qab=0.4J ③ (1分)
Qcd =I2Rcdt ④ (1分) Qab + QR =I2RRabt/(Rab+R) ⑤(1分)
联立④⑤可得Qab =0.9J ⑥ (1分)
(2) 细绳被拉断瞬时,对ab棒有:
Fm=mg+BIabL ⑦ (2分)
又有IR=RabIab/R ⑧ ( 1分) Icd=Iab+Icd ⑨ (1分)
又由闭合欧姆定可得 BLv=Icd [Rcd+RabR/(Rab+R)] ⑩ (2分)
联立⑦⑧⑨⑩可得v=
(3)由功能关系得 Mgh= Q总 +mv2/2 ?(4分)
即可得h=
13、(20分)(1)设第一颗子弹进入靶盒A后,子弹与靶盒A共同速度为υ1。
根据碰撞过程系统动量守恒,有mυ0=(m+M)υ1 ………………………………………………①
设A离开O点的最大距离为s1,根据动能定理有:-Fs1=0-(m+M)理科综合.files/image122.gif) …………………②
…………………②
由①、②式得s1=
评分标准:①、②、③式各2分。
(2)根据题意,A在恒力F作用下返回O点时第二颗子弹打入,由于A的动量与第二颗子弹
动量大小相同、方向相反,第二颗子弹打入后A将静止在O点。设第三颗子弹打入A后,它
们的共同速度为υ3
由系统动量守恒:理科综合.files/image124.gif) ………………………………………………………………④
………………………………………………………………④
设A从离开O点到又回到O点经历时间为t,且碰后A运动方向为正方向,
由动量定理得:理科综合.files/image126.gif) …………………………………………………………⑤
…………………………………………………………⑤
由④、⑤两式得:t=0.5s……………………………………………………………………………⑥
评分标准:必要文字叙述1分,④、⑤、⑥三式各2分。
(3)设B至少发射n颗子弹,且碰后A的速度为υn
由系统动量守恒:理科综合.files/image128.gif) ………………………………………………………………⑦
………………………………………………………………⑦
由动能定理:理科综合.files/image130.gif) ……………………………………………………………⑧
……………………………………………………………⑧
根据题意:sn<
由⑦、⑧、⑨式得:n>27,所以B至少发射28颗子弹…………………………………………⑩
评分标准:⑨式1分,其余各式各2分。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com