
题目列表(包括答案和解析)
(23分)如图为一传送装置,倾角为α=53°的斜面AB与水平传送带在B处由一光滑小圆弧平滑衔接,可看作质点的货物从斜面上A点由静止下滑,经长度为S1的传送带后,最后抛入固定于水平地面上的圆弧形槽内。已知物体与斜面、传送带间的滑动摩擦因数均为μ=0.5,传送带两皮带轮的半径均为R1=0.4m,传送带上表面BC离地的高度h=1.2m。圆弧槽半径R2=1m,两边缘与圆心连线与竖直方向的夹角均为β=53°。当传送带静止时,将货物在斜面上离B点S2远处静止释放,货物脱离传送带后刚好沿圆弧槽左边缘D点的切线方向飞入槽内。当传送带顺时针转动时,无论传送带转多快,货物也不会从圆弧槽右边缘飞出,求:

(1)传送带静止时,货物到达C点的速度大小和D点时的速度大小。
(2)求S1、S2的值应满足的关系。(sin53°= 0.8,cos53°= 0.6 )
(23分)如图为一传送装置,倾角为α=53°的斜面AB与水平传送带在B处由一光滑小圆弧平滑衔接,可看作质点的货物从斜面上A点由静止下滑,经长度为S1的传送带后,最后抛入固定于水平地面上的圆弧形槽内。已知物体与斜面、传送带间的滑动摩擦因数均为μ=0.5,传送带两皮带轮的半径均为R1=0.4m,传送带上表面BC离地的高度h=1.2m。圆弧槽半径R2=1m,两边缘与圆心连线与竖直方向的夹角均为β=53°。当传送带静止时,将货物在斜面上离B点S2远处静止释放,货物脱离传送带后刚好沿圆弧槽左边缘D点的切线方向飞入槽内。当传送带顺时针转动时,无论传送带转多快,货物也不会从圆弧槽右边缘飞出,求: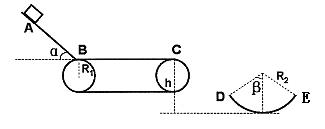
(1)传送带静止时,货物到达C点的速度大小和D点时的速度大小。
(2)求S1、S2的值应满足的关系。(sin53°= 0.8,cos53°= 0.6 )
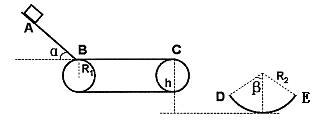
题23图所示为一种摆式摩擦因数测量仪,可测量轮胎与地面间动摩擦因数,其中主要部件有:底部固定有轮胎橡胶片的摆锤和连接摆锤的轻质细杆。摆锤的质量为m,细杆可绕轴O在竖直平面内自由转动,摆锤重心到O点的距离为L.测量时,测量仪固定于水平地面,将摆锤从与0等高的位置由静止释放。摆锤到最低点附近时,橡胶片紧压地面擦过一小段距离s(s<<L),之后继续摆动至与坚直方向成θ角的最高位置。若摆锤对地面的压力可视为大小为F的恒力,重力加速度为g,求
⑴摆锤在上述过程中损失的机械能
⑵在上述过程中摩擦力对摆锤所做的功
⑶橡胶片与地面间的动摩擦因数
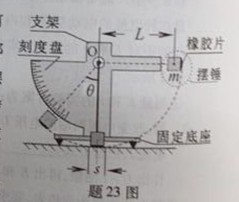
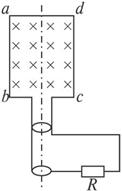
图23
(1)外电阻R上产生的焦耳热Q;
(2)这段时间内通过外电阻R的电荷量.
1.B 解析:.files/image003.gif) 转变成可裂变的
转变成可裂变的.files/image005.gif) (金属钚),质量数增加1,一定是吸收一个快中子变成铀239,再转变成
(金属钚),质量数增加1,一定是吸收一个快中子变成铀239,再转变成.files/image005.gif) 时核电荷数增加2,因此是发生了两次β衰变,AC错B正确;钚239是中子数为239-94=145,铀238的中子数为238-92=146,因此钚239比铀238少一个中子,D错。
时核电荷数增加2,因此是发生了两次β衰变,AC错B正确;钚239是中子数为239-94=145,铀238的中子数为238-92=146,因此钚239比铀238少一个中子,D错。
2.B 解析:随水银柱上升,水银柱的长度变短,气体压强变小,当水银被全部推出管外后,气体压强等于大气压强为最小,A错;水银柱缓慢上升时,气体温度升高,内能增大,同时气体体积增大,对外做功,由.files/image182.gif) 可知,
可知,.files/image184.gif) ,B正确;在水银被从管中突然全部推出过程中,气体迅速膨胀对外做功,但吸热较慢因此气体的内能一定减小,C错;若在端面a上升到
,B正确;在水银被从管中突然全部推出过程中,气体迅速膨胀对外做功,但吸热较慢因此气体的内能一定减小,C错;若在端面a上升到.files/image008.gif) 前停止加热,气体温度下降,V减小,水银柱下降,但当气体温度回到初始状态时,压强比初始状态小,气体柱比初始状态长,D错。
前停止加热,气体温度下降,V减小,水银柱下降,但当气体温度回到初始状态时,压强比初始状态小,气体柱比初始状态长,D错。
.files/image186.gif) 3.AC 解析:由图可知,
3.AC 解析:由图可知,.files/image021.gif) 车的初速度等于
车的初速度等于.files/image189.gif) ,在
,在.files/image031.gif) 时间内,
时间内,.files/image021.gif) 车的位移为
车的位移为.files/image028.gif) ,则
,则.files/image019.gif) 车的位移为
车的位移为.files/image195.gif) 。若
。若.files/image013.gif) 在
在.files/image031.gif) 时刻相遇,则
时刻相遇,则.files/image199.gif) ,A项正确;若
,A项正确;若.files/image013.gif) 在
在.files/image036.gif) 时刻相遇,由图象可知,
时刻相遇,由图象可知,.files/image028.gif) 为阴影部分对应的距离,即
为阴影部分对应的距离,即.files/image204.gif) ,由图象中的对称关系,下次相遇的时刻为
,由图象中的对称关系,下次相遇的时刻为.files/image206.gif) ,C正确B项错;若
,C正确B项错;若.files/image013.gif) 在
在.files/image031.gif) 时刻相遇,之后
时刻相遇,之后.files/image210.gif) ,不能再次相遇,D错。
,不能再次相遇,D错。
.files/image211.gif) 4.B 解析:在物块下滑过程中重力对物块的冲量为15N?s,故下滑时间为
4.B 解析:在物块下滑过程中重力对物块的冲量为15N?s,故下滑时间为.files/image213.gif) s,斜面对物块的支持力
s,斜面对物块的支持力.files/image215.gif) N,故支持力的冲量
N,故支持力的冲量.files/image217.gif) ,A错;物块从静止下滑,斜面对物块的滑动摩擦力
,A错;物块从静止下滑,斜面对物块的滑动摩擦力.files/image219.gif) N,其冲量为
N,其冲量为.files/image221.gif) ,B正确;斜面对物块的作用力一定小于物块的重力,所以其冲量一定小于重力的冲量,C错;物块到达斜面底端时的动量等于外力的总冲量,一定小于重力的冲量,D错。
,B正确;斜面对物块的作用力一定小于物块的重力,所以其冲量一定小于重力的冲量,C错;物块到达斜面底端时的动量等于外力的总冲量,一定小于重力的冲量,D错。
5.C 解析:水流做平抛运动,水平位移.files/image223.gif) ,代入
,代入.files/image056.gif) 解得
解得.files/image226.gif) ,即得
,即得.files/image228.gif) (d>0,舍去),因此当H一定时,
(d>0,舍去),因此当H一定时,.files/image230.gif) 与
与.files/image054.gif) 有关,A错;若
有关,A错;若.files/image054.gif) 一定,则H减小时d增大,B错;若H一定,
一定,则H减小时d增大,B错;若H一定,.files/image054.gif) 增大时,d也应该增大,C正确;若d一定,H减小时,
增大时,d也应该增大,C正确;若d一定,H减小时,.files/image054.gif) 应该减小,D错。
应该减小,D错。
.files/image235.gif)
.files/image236.gif) 6.ACD 解析:对A、B整体和P,受力如图(a)(b),其中
6.ACD 解析:对A、B整体和P,受力如图(a)(b),其中.files/image238.gif)
.files/image240.gif) ,
, .files/image242.gif)
.files/image244.gif) 。若保持B的半径
。若保持B的半径.files/image072.gif) 不变,而将B改变密度较大的材料制作,则
不变,而将B改变密度较大的材料制作,则.files/image153.gif) 角不变而B的质量增大,
角不变而B的质量增大,.files/image248.gif) 均增大,A正确;对B,受力如图(c),
均增大,A正确;对B,受力如图(c),.files/image250.gif) ,
,.files/image252.gif) ,设墙对A的支持力为
,设墙对A的支持力为.files/image254.gif) 。若保持A的质量
。若保持A的质量.files/image074.gif) 不变,而将A改用密度稍小的材料制作,则A的半径增大,
不变,而将A改用密度稍小的材料制作,则A的半径增大,.files/image257.gif) 角减小,
角减小,.files/image259.gif) 增大,C正确;(
增大,C正确;(.files/image153.gif) 减小,
减小,.files/image262.gif) 减小,
减小,.files/image264.gif) 减小,)。 若保持B的质量
减小,)。 若保持B的质量.files/image077.gif) 不变,而将B改用密度较小的材料制作,则B的半径增大,
不变,而将B改用密度较小的材料制作,则B的半径增大,.files/image257.gif) 增大,
增大,.files/image259.gif) 减小,
减小,.files/image153.gif) 不变,
不变,.files/image268.gif) 不变,
不变,.files/image264.gif) 增大,D正确。
增大,D正确。
.files/image270.gif) 7.B 解析: O点第一次达到正方向最大位移所需时间为
7.B 解析: O点第一次达到正方向最大位移所需时间为.files/image272.gif) ,因此波向前传播的距离为
,因此波向前传播的距离为.files/image274.gif) ,即OP、OP’为
,即OP、OP’为.files/image274.gif) ,因此P、P’两点间距离为半个波长,但由于波是以O为波源向左右传播的,左右对称点振动总相同如图
,因此P、P’两点间距离为半个波长,但由于波是以O为波源向左右传播的,左右对称点振动总相同如图.files/image277.gif) ,因此O点振动时间为
,因此O点振动时间为.files/image279.gif) ,所走路程为
,所走路程为.files/image281.gif) cm,B正确;波动传播的是振动的运动形式,质点并不沿传播方向向前传播,C错;同种波在同一介质中传播的速度是相同的,即
cm,B正确;波动传播的是振动的运动形式,质点并不沿传播方向向前传播,C错;同种波在同一介质中传播的速度是相同的,即.files/image283.gif) ,当O质点振动周期减为2s,则O第一次达到正方向最大位移的时间为0.5s,波向左、右传播的距离为
,当O质点振动周期减为2s,则O第一次达到正方向最大位移的时间为0.5s,波向左、右传播的距离为.files/image285.gif) ,P点还没有振动,D错.
,P点还没有振动,D错.
8.BD 9.D 10.A
11.AD 解析:AD两图中,当滑动变阻器的滑动触头放在最左端时,电源被短路而烧坏;BC两图中,供电电路正确,B图虽然电流表和电压表接错位置,但由于串联的电压表内阻较大,不会烧坏电流表;C图则可测较大电阻的阻值。
12.(1)作图法 ;(2)画出.files/image287.gif) 的s-t图(如图线甲)和
的s-t图(如图线甲)和.files/image100.gif) 的s-t图(如图线乙)
的s-t图(如图线乙)
.files/image290.jpg) 在误差允许的范围内,图线甲为直线,物体从A到B的运动为匀速直线运动,从图线的斜率可求得:
在误差允许的范围内,图线甲为直线,物体从A到B的运动为匀速直线运动,从图线的斜率可求得:.files/image292.gif) ,
,
.files/image294.gif)
从乙图中无法直接判断s、t之间的关系,但是该图线接近于二次函数的图像。为了验证这个猜想,通过转换变量来进行,即作s-t2图线,为此求得表格如下:
.files/image100.gif)
时间t(s)
0.89
1.24
1.52
1.76
1.97
新变量t2(s2)
0.79
1.54
2.31
3.10
3.88
位移s(m)
0.25
0.50
0.75
1.00
1.25
依据上表中的t2、、s数据可作图线丙。从图像中看出s与t2、呈线性变化关系,由图中斜率求得,即.files/image297.gif) 故
故.files/image299.gif)
(3)从.files/image287.gif) 的过程中s随t变化的规律是:
物体作匀速直线运动,
的过程中s随t变化的规律是:
物体作匀速直线运动,.files/image294.gif)
从.files/image100.gif) 的过程中s随t变化的规律是:物体作初速度为零的匀加速直线运动,
的过程中s随t变化的规律是:物体作初速度为零的匀加速直线运动,.files/image304.gif)
13.解析:对质子火箭发动机,加速每一个质子的过程
.files/image306.gif) ①
①
对任意一段时间.files/image308.gif) 内通过质子的总电荷量为q,总质量为M,由能量关系:
内通过质子的总电荷量为q,总质量为M,由能量关系:
.files/image310.gif) ②
②
由动量定理得 .files/image312.gif) ③
③
联立①②③解得
.files/image314.gif) ④
④
14.(1)轮缘转动的线速度:.files/image316.gif) (2分)
(2分)
(2)板运动的加速度:.files/image318.gif) (2分)
(2分)
板在轮子上做匀加速运动的时间:.files/image320.gif) (1分)
(1分)
板在做匀加速运动的全过程中其重心平动发生的位移为:
.files/image322.gif) (1分)
(1分)
板在做匀速运动的全过程中其重心平动发生的位移为:
.files/image324.gif) (1分)
(1分)
因此,板运动的总时间为:.files/image326.gif) (2分)
(2分)
(3)由功能关系知:轮子在传送木板的过程中所消耗 的机械能一部分转化成了木板的动能,另一部分因克服摩擦力做功转化成了内能,即:
木板获得的动能:.files/image328.gif) (1分)
(1分)
摩擦力做功产生的内能:.files/image330.gif) (2分)
(2分)
加速过程木板与轮子间的相对位移:
.files/image332.gif) (1分)
(1分)
消耗的机械能:.files/image334.gif) (2分)
(2分)
联立上述四个方程解得:
.files/image336.gif) (1分)
(1分)
15.解析:⑴正、负电子均经过.files/image124.gif) 次加速后才从加速器射出,故
次加速后才从加速器射出,故
.files/image339.gif) ①
①
.files/image341.gif) ②
②
⑵.files/image031.gif) 时刻
时刻.files/image344.gif) 负,在
负,在.files/image346.gif) 之间加速正电子,则
之间加速正电子,则.files/image348.gif) 时刻在
时刻在.files/image346.gif) 之间加速负电子,且正、负电子在加速器中运动的时间相同,因此射出的时间差即为
之间加速负电子,且正、负电子在加速器中运动的时间相同,因此射出的时间差即为.files/image351.gif) ③
③
⑶由于金属圆筒的静电屏蔽作用,筒内场强为零,电子在每个圆筒中都做匀速运动,要使电子每经过两筒缝隙时都能被加速,运动时间应满足.files/image353.gif) ④
④
电子第一次被加速后的速度即通过.files/image355.gif) 时的速度,因此
时的速度,因此
.files/image357.gif) ⑤
⑤
同理可得
.files/image359.gif)
.files/image361.gif)
…………
解得
.files/image363.gif)
16.解析:⑴设导体棒MN下滑的距离为.files/image164.gif) ,导体棒下滑时受三个力如图所示,由牛顿第二定律得
,导体棒下滑时受三个力如图所示,由牛顿第二定律得 .files/image366.gif) ①
①
.files/image368.gif) ②
②
线框.files/image144.gif) 被导体棒MN分成并联的两部分,对MN两端的总电阻为
被导体棒MN分成并联的两部分,对MN两端的总电阻为
.files/image370.gif)
.files/image372.gif) ③
③
将.files/image166.gif) 时速度为
时速度为.files/image168.gif) 代入得
代入得 .files/image376.gif) ④
④
⑵当导体棒的加速度为零时,由①得 .files/image378.gif) ⑤
⑤
由②③代入.files/image170.gif) 得
得 .files/image381.gif) ⑥
⑥
联立⑤⑥得 .files/image383.gif) ⑦
⑦
⑶假设导体棒以速度.files/image172.gif) 匀速运动,虽然磁感应强度方向与区域Ⅰ中相反,但由楞次定律和左手定则可知,安培力仍沿斜面向上,则有
匀速运动,虽然磁感应强度方向与区域Ⅰ中相反,但由楞次定律和左手定则可知,安培力仍沿斜面向上,则有
.files/image386.gif) ⑧
⑧
由于.files/image388.gif) 为常量,因此当
为常量,因此当.files/image390.gif) 时
时.files/image392.gif) 最大,而式中
最大,而式中.files/image394.gif) ,因此当
,因此当.files/image164.gif) 增大时
增大时.files/image392.gif) 减小,若
减小,若.files/image174.gif) 不变,则速度一定减小,要保持速度不变,则由⑦⑧得
不变,则速度一定减小,要保持速度不变,则由⑦⑧得
.files/image399.gif) ⑨
⑨
.files/image401.gif) ⑩
⑩
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com