C．选修4—4：坐标系与参数方程
(本小题满分10分)
在极坐标系中，圆的方程为，以极点为坐标原点，极轴为轴的正半轴建立平面直角坐标系，直线的参数方程为（为参数），判断直线和圆的位置关系．

C．选修4-4：坐标系与参数方程（本小题满分10分）
在平面直角坐标系中，求过椭圆（为参数）的右焦点且与直线（为参数）平行的直线的普通方程。

C．（选修4—4：坐标系与参数方程）

在极坐标系中，圆的方程为，以极点为坐标原点，极轴为轴的正

半轴建立平面直角坐标系，直线的参数方程为（为参数），求直线被截

得的弦的长度.

C．（坐标系与参数方程选做题）已知极坐标的极点在直角坐标系的原点O处，极轴与x轴的正半轴重合，曲线C的参数方程为（为参数），直线l的极坐标方程为．点P在曲线C上，则点P到直线l的距离的最小值为                 ．

C．选修4－4：坐标系与参数方程

在直角坐标系中，已知曲线的参数方程是（是参数），若以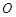为极点，轴的正半轴为极轴，取与直角坐标系中相同的单位长度，建立极坐标系，求曲线的极坐标方程．