
题目列表(包括答案和解析)
| C | n 2n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 0 n |
| C | n n |
| C | 1 n |
| C | n-1 n |
| C | 2 n |
| C | n-2 n |
| C | n n |
| C | 0 n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | n 2n |
| C | 0 2n |
| C | 1 2n |
| C | 2 2n |
| C | 3 2n |
| C | 2n 2n |
| C | n 2n |
| C | n 2n |
我们常用构造等式对同一个量算两次的方法来证明组合恒等式,如由等式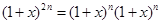 可得,左边
可得,左边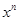 的系数为
的系数为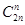 ,
,
而右边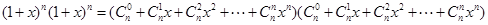 ,
, 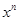 的系数为
的系数为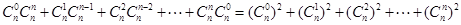 ,
,
由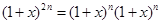 恒成立,可得
恒成立,可得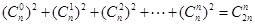 .
.
利用上述方法,化简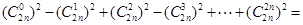 .
.
| C | n2n |
| C | 0n |
| C | 1n |
| C | 2n |
| C | nn |
| C | 0n |
| C | 1n |
| C | 2n |
| C | nn |
| C | 0n |
| C | nn |
| C | 1n |
| C | n-1n |
| C | 2n |
| C | n-2n |
| C | nn |
| C | 0n |
| C | 0n |
| C | 1n |
| C | 2n |
| C | nn |
| C | 0n |
| C | 1n |
| C | 2n |
| C | nn |
| C | n2n |
| C | 02n |
| C | 12n |
| C | 22n |
| C | 32n |
| C | 2n2n |
 (2013•泰安二模)如图,一个由两个圆锥组合而成的空间几何体的正视图和侧视图都是边长为1、一个内角为60°的菱形,俯视图是圆及其圆心,那么这个几何体的体积为( )
(2013•泰安二模)如图,一个由两个圆锥组合而成的空间几何体的正视图和侧视图都是边长为1、一个内角为60°的菱形,俯视图是圆及其圆心,那么这个几何体的体积为( )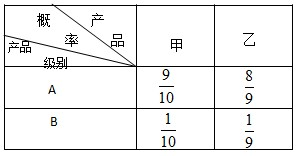 (2010•合肥模拟)某企业生产一种风险较大的高科技产品M,要用甲和乙两种初级产品组合而成,甲和乙两种初级产品生产相互独立,每种初级产品生产结果均有A、B两个等级. 若随机的选用甲、乙两种初级产品各一个组装成一个产品M,甲和乙两种初级产品均为A级时组合而成产品M为合格品,其余均为次品.该厂在生产甲和乙两种初级产品时的等级概率如表:
(2010•合肥模拟)某企业生产一种风险较大的高科技产品M,要用甲和乙两种初级产品组合而成,甲和乙两种初级产品生产相互独立,每种初级产品生产结果均有A、B两个等级. 若随机的选用甲、乙两种初级产品各一个组装成一个产品M,甲和乙两种初级产品均为A级时组合而成产品M为合格品,其余均为次品.该厂在生产甲和乙两种初级产品时的等级概率如表:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com