
题目列表(包括答案和解析)
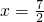 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).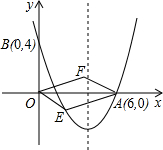 行四边形?若能,求出点E、F的坐标;若不能,请说明理由.(第(4)问不写解答过程,只写结论)
行四边形?若能,求出点E、F的坐标;若不能,请说明理由.(第(4)问不写解答过程,只写结论) 的抛物线经过点A(6,0)和B(0,4)。
的抛物线经过点A(6,0)和B(0,4)。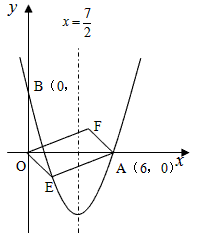
如图,对称轴为直线![]() 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).

1.求抛物线解析式及顶点坐标;
2.设点E(x,y)是抛物线第四象限上一动点,四边形OEAF是以OA为对角线的平行四边形,求 OEAF的面积S与x之间的函数关系式,并求出自变量的取值范围
OEAF的面积S与x之间的函数关系式,并求出自变量的取值范围
3.若S=24,试判断![]() OEAF是否为菱形。
OEAF是否为菱形。
4.若点E在⑴中的抛物线上,点F在对称轴上,以O、E、A、F为顶点的四边形能否为平行四边形,若能,求出点E、F的坐标;若不能,请说明理由。(第⑷问不写解答过程,只写结论)
(12分)如图,对称轴为直线![]() 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
1.⑴求抛物线解析式及顶点坐标;
2.⑵设点E(x,y)是抛物线第四象限上一动点,四边形OEAF是以OA为对角线的平行四边形,求![]() OEAF的面积S与x之间的函数关系式,并求出自变量的取值范围;
OEAF的面积S与x之间的函数关系式,并求出自变量的取值范围;
3.⑶若S=24,试判断![]() OEAF是否为菱形。
OEAF是否为菱形。
4.⑷若点E在⑴中的抛物线上,点F在对称轴上,以O、E、A、F为顶点的四边形能否为平行四边形,若能,求出点E、F的坐标;若不能,请说明理由。(第⑷问不写解答过程,只写结论)

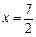 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).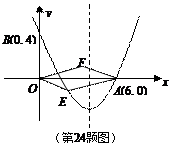
 OEAF的面积S与x之间的函数关系式,并求出自变量的取值范围
OEAF的面积S与x之间的函数关系式,并求出自变量的取值范围 OEAF是否为菱形。
OEAF是否为菱形。一、1.B 2.C 3.C 4.B 5.D 6.D
二、7、 8、-2<x<3 9、SSS
10、∏
11、22.5° 12、5
8、-2<x<3 9、SSS
10、∏
11、22.5° 12、5
13、2 14、20 15、15
三、16.(1) (2)化简结果为
(2)化简结果为 (求值时除tang45°外都可带入)
(求值时除tang45°外都可带入)
17.(略)
18.(1)6% 144 ----------2分
(2)甲的平均成绩72×40%+98×40%+60×20%=92(分)----------4分
乙的平均成绩 90×40%+75×40%+95×20%=85(分) ---------6分
所以他们俩都达到优秀生水平;
(3)(回答只要合理就给分) -----------------8分
19、(1)(略) --------------------5分
(2) --------------------9分
--------------------9分
20、0.2小时
21、(1)略 ------------4分
(2) ---------------9分
---------------9分
22(1) -------------------3分
-------------------3分
(2)定价为3元较为合适 ----------------7分
(3)当定价为3.5元时利润最大--------11分
23.解:(1)抛物线 的解析式为
的解析式为 -------------------3分.
-------------------3分.
(可利用一般式、顶点式、对称性关系等方法解答)
(2)当动点B运动到为 顶点时,平行四边形ABCD是菱形,此时点D恰好是抛物线
顶点时,平行四边形ABCD是菱形,此时点D恰好是抛物线 的解析式为
的解析式为 的定点,
---------------5分
的定点,
---------------5分
 ,
, ,
-------------------6分
,
-------------------6分
所以: .
------------------7分
.
------------------7分
 (3)
(3)
 能为矩形.-------------8分
能为矩形.-------------8分
过点 作
作 轴于
轴于 ,由点
,由点 在
在 上,可设点
上,可设点 的坐标为
的坐标为 ,
,
则 ,
, .
.
易知,当且仅当 时,
时, 为矩形.
为矩形.
在 中,由勾股定理得,
中,由勾股定理得, ,---------------9分
,---------------9分
 ,
, (舍去),
(舍去), .
.
所以,当点 坐标为
坐标为 或
或 时,
时, 为矩形, -----------------10分
为矩形, -----------------10分
此时,点 的坐标分别是
的坐标分别是 .
.
因此,符合条件的矩形有且只有2个,即矩形 和矩形
和矩形 .
.
设直线 与
与 轴交于
轴交于 ,显然,
,显然, ,
,
 ,
, .
.

由该图形的对称性知矩形 与矩形
与矩形 重合部分是菱形,
重合部分是菱形,
其面积为 .---------11分
.---------11分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com