
题目列表(包括答案和解析)
(2011四川内江,17,7分)计算: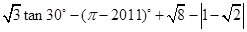
(2011四川内江,3,3分)某红外线遥控器发出的红外线波长为0.000 000 94m,用科学记数法表示这个数是( )
A.9.4×10-7 m B.9.4×107m C.9.4×10-8m D.9.4×108m
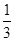 n(n+1)(n—1)时,我们可以这样做:
n(n+1)(n—1)时,我们可以这样做: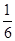 ×
× (2011四川内江,17,7分)计算:![]()
(2011四川内江,15,5分)如果分式 的值为0,则x的值应为
.
的值为0,则x的值应为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com