
题目列表(包括答案和解析)
已知数列 是首项为
是首项为 的等比数列,且满足
的等比数列,且满足
 .
.
(1) 求常数 的值和数列
的值和数列 的通项公式;
的通项公式;
(2) 若抽去数列 中的第一项、第四项、第七项、……、第
中的第一项、第四项、第七项、……、第 项、……,余下的项按原来的顺序组成一个新的数列
项、……,余下的项按原来的顺序组成一个新的数列 ,试写出数列
,试写出数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,设数列 的前
的前 项和为
项和为 .是否存在正整数
.是否存在正整数 ,使得
,使得 ?若存在,试求所有满足条件的正整数
?若存在,试求所有满足条件的正整数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问中解:由 得
得 ,,
,,
又因为存在常数p使得数列 为等比数列,
为等比数列,
则 即
即 ,所以p=1
,所以p=1
故数列 为首项是2,公比为2的等比数列,即
为首项是2,公比为2的等比数列,即 .
.
此时 也满足,则所求常数
也满足,则所求常数 的值为1且
的值为1且
第二问中,解:由等比数列的性质得:
(i)当 时,
时, ;
;
(ii) 当 时,
时, ,
,
所以
第三问假设存在正整数n满足条件,则 ,
,
则(i)当 时,
时,
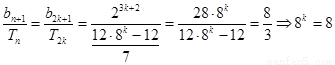
 ,
,
(1)求首项a1和公比q,并写出an的通项公式;
(2)如果数列{cn}满足![]() (n∈N*),求数列{cn}的前n项之和Sn.
(n∈N*),求数列{cn}的前n项之和Sn.
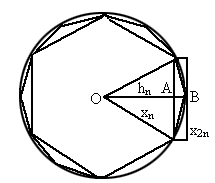
如图,设圆的半径为1,弦心距为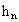 ;正n边形的边长为
;正n边形的边长为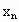 ,面积为
,面积为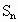 .由勾股定理,得
.由勾股定理,得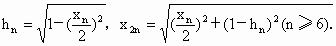
容易知道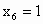 .
.
观察图1,不难发现,正2n边形的面积等于正n边形的面积加上n个等腰三角形的面积,即
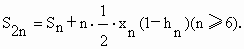
利用这个递推公式,我们可以得到:
正六边形的面积
正十二边形的面积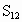 ________;
________;
正二十四边形的面积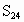 ________;
________;
…
请问n的输入值满足什么条件?n的输出组表示什么?当n不断增大,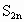 的值不断趋近于什么?用循环结构编写出程序,还用Scilab语言编写一个程序.
的值不断趋近于什么?用循环结构编写出程序,还用Scilab语言编写一个程序.
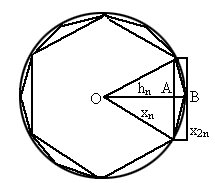
如图,设圆的半径为
1,弦心距为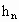 ;正n边形的边长为
;正n边形的边长为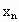 ,面积为
,面积为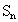 .由勾股定理,得
.由勾股定理,得
容易知道
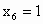 .
.
观察图
1,不难发现,正2n边形的面积等于正n边形的面积加上n个等腰三角形的面积,即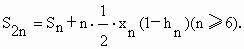
利用这个递推公式,我们可以得到:
正六边形的面积
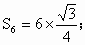
正十二边形的面积
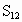 ________;
________;
正二十四边形的面积
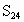 ________;
________;
…
请问
n的输入值满足什么条件?n的输出组表示什么?当n不断增大,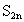 的值不断趋近于什么?用循环结构编写出程序,还用Scilab语言编写一个程序.
的值不断趋近于什么?用循环结构编写出程序,还用Scilab语言编写一个程序.
某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组 数 | 分 组 | 低碳族的人数 | 占本组的频率 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 | p |
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) | a | 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55] | 15 | 0.3 |
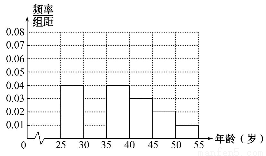
(1)补全频率分布直方图并求n,a,p的值.
(2)为调查该地区的年龄与生活习惯和是否符合低碳观念有无关系,调查组按40岁以下为青年,40岁以上(含40岁)为老年分成两组,请你先完成下面2×2列联表,并回答是否有99%的把握认为该地区的生活习惯是否符合低碳观念与人的年龄有关.
参考公式:χ2=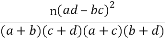
P(χ2≥x0) | 0.050 | 0.010 | 0.001 |
x0 | 3.841 | 6.635 | 10.828 |
年龄组
是否低碳族 | 青 年 | 老 年 | 总 计 |
低碳族 |
|
|
|
非低碳族 |
|
|
|
总计 |
|
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com