（1）要使两球在B球上升过程中相遇，则v₀应满足什么条件？

（2）要使两球在B球下降过程中相遇，则v₀应满足什么条件？

A球自距地面高h处开始自由下落，同时B球以初速度v₀正对A球竖直上抛，空气阻力不计。问：

（1）要使两球在B球上升过程中相遇，则v₀应满足什么条件？?

（2）要使两球在B球下降过程中相遇，则v₀应满足什么条件？

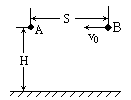
两个小球A和B，处在离地面H＝20米的高处的同一水平面上，相距为s＝10米．在A球开始自由下落的同时，B球以v₀的水平初速度对着A球抛去(如图所示)．要在A球下落5米后两球相遇，B球初速度v₀的取值范围应如何？(g取10米/秒²)

㈠

某同学利用光电门传感器设计了一个研究小物体自由下落时机械能是否守恒的实验，实验装置如图所示，图中A、B两位置分别固定了两个光电门传感器。实验时测得小物体上宽度为d的挡光片通过A的挡光时间为t₁，通过B的挡光时间为t₂。为了证明小物体通过A、B时的机械能相等，还需要进行一些实验测量和列式证明。

⑴选出下列必要的实验测量步骤

A.用天平测出运动小物体的质量m

B.测出A、B两传感器之间的竖直距离h

C.测出小物体释放时离桌面的高度H

D.用秒表测出运动小物体通过A、B两传感器的时间△t

⑵若该同学用d和t的比值来反映小物体经过A、B光电门时的速度，并设想如果能满足________________________关系式，即能证明在自由落体过程中小物体的机械能是守恒的。

⑶该同学的实验设计可能会引起明显误差的地方是(请写出一种)： _____________。

㈡物体在空中下落的过程中，重力做正功，物体的动能越来越大，为了“探究重力做功和物体动能变化间的定量关系”，我们提供了如下图的实验装置。

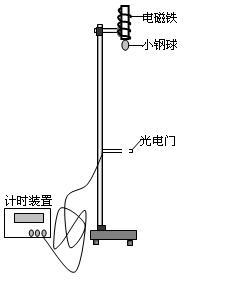
⑴某同学根据所学的知识结合右图设计一个本实验情景的命题：

如图所示，设质量为m（已测定）的小球在重力mg作用下从开始端自由下落至光电门发生的 　①　 ，通过光电门时的　②　，试探究外力做的功　③　与小球动能变化量

④  的定量关系。(请在①②空格处填写物理量的名称和对应符号；在③④空格处填写数学表达式。)

⑵某同学根据上述命题进行如下操作并测出如下数字。

①用天平测定小球的质量为0.50kg；

②用游标尺测出小球的直径为10.0mm；

③用刻度尺测出电磁铁下端到光电门的距离为80.80cm；

④电磁铁先通电，让小球             。

⑤　        　，小球自由下落。

⑥在小球经过光电门时间内，计时装置记下小球经过光电门所用时间为2.50×10^－3s，由此可算得小球经过光电门时的速度为　    　m/s。

⑦计算得出重力做的功为　   　J，小球动能变化量为　      J。(g取10m/s²，结果保留三位有效数字)

⑶试根据在⑵条件下做好本实验的结论：　                 。