
题目列表(包括答案和解析)
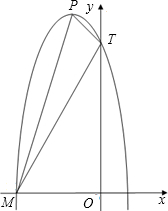 如图,已知抛物线y=-3x2-(2c-b)x+a2,其中a、b、c是一个直角三角形的三边的长,且a<b<c,又知这个三角形两锐角的正弦值分别是方程25x2-35x+12=0的两个根.
如图,已知抛物线y=-3x2-(2c-b)x+a2,其中a、b、c是一个直角三角形的三边的长,且a<b<c,又知这个三角形两锐角的正弦值分别是方程25x2-35x+12=0的两个根.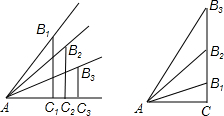 (1)如图锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(1)如图锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律. (1)如图,在锐角三角形ABC中,BC=12,sinA=
(1)如图,在锐角三角形ABC中,BC=12,sinA=| 3 | 4 |
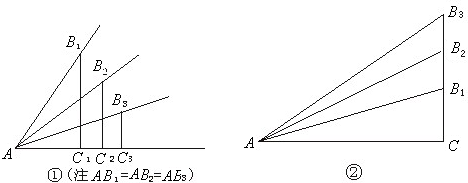
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com