
题目列表(包括答案和解析)
已知 是互不相等的非零实数,求证:由
是互不相等的非零实数,求证:由 确定的三条抛物线至少有一条与
确定的三条抛物线至少有一条与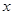 轴有两个不同的交点.
轴有两个不同的交点.
【解析】本试题主要是考查了运用反证法思想,对于正面解决难的问题的运用。
| ||
| 2 |
| A、甲批次的总体平均数与标准值更接近 |
| B、乙批次的总体平均数与标准值更接近 |
| C、两个批次总体平均数与标准值接近程度相同 |
| D、两个批次总体平均数与标准值接近程度不能确定 |
已知函数 ,
, ,k为非零实数.
,k为非零实数.
(Ⅰ)设t=k2,若函数f(x),g(x)在区间(0,+∞)上单调性相同,求k的取值范围;
(Ⅱ)是否存在正实数k,都能找到t∈[1,2],使得关于x的方程f(x)=g(x)在[1,5]上有且仅有一个实数根,且在[-5,-1]上至多有一个实数根.若存在,请求出所有k的值的集合;若不存在,请说明理由.
【解析】本试题考查了运用导数来研究函数的单调性,并求解参数的取值范围。与此同时还能对于方程解的问题,转化为图像与图像的交点问题来长处理的数学思想的运用。
(2009四川卷文)设矩形的长为![]() ,宽为
,宽为![]() ,其比满足
,其比满足![]() ∶
∶![]() =
=![]() ,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是
A. 甲批次的总体平均数与标准值更接近
B. 乙批次的总体平均数与标准值更接近
C. 两个批次总体平均数与标准值接近程度相同
D. 两个批次总体平均数与标准值接近程度不能确定
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com