
题目列表(包括答案和解析)
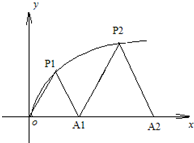 如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn) 是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn) 是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).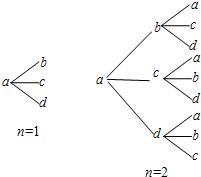 用a,b,c,d四个不同字母组成一个含n+1(n∈N+)个字母的字符串,要求由a开始,相邻两个字母不同.例如n=1时,排出的字符串是ab,ac,ad;n=2时排出的字符串是aba,abc,abd,aca,acb,acd,ada,adb,adc,…,如图所示.记这含n+1个字母的所有字符串中,排在最后一个的字母仍是a的字符串的种数为an.
用a,b,c,d四个不同字母组成一个含n+1(n∈N+)个字母的字符串,要求由a开始,相邻两个字母不同.例如n=1时,排出的字符串是ab,ac,ad;n=2时排出的字符串是aba,abc,abd,aca,acb,acd,ada,adb,adc,…,如图所示.记这含n+1个字母的所有字符串中,排在最后一个的字母仍是a的字符串的种数为an.| 3n+3(-1)n |
| 4 |
| 2 |
| 9 |
| 1 |
| 3 |
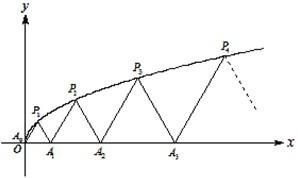 如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).| 1 |
| 2n |
|
| 2m-1 |
| 2n |
(本小题12分)
如图, <
< <
< <…<
<…< )是曲线C
)是曲线C
 :
: 上的n个点,点
上的n个点,点 在x轴的正半轴上,且⊿
在x轴的正半轴上,且⊿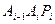 是正三角形(
是正三角形( 是坐标原点)。
是坐标原点)。
(1)写出
(2)求出点 的横坐标
的横坐标 关于n的表达式并用数学归纳法证明
关于n的表达式并用数学归纳法证明
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com