练习册

  • 练习册
  • 试题
    26．如图.已知直线的解析式为.直线与x轴.y轴分别相交于A.B两点.直线经过B.C两点.点C的坐标为(8.0).又已知点P在x轴上从点A向点C移动.点Q在直线从点C向点B移动.点P.Q同时出发.且移动的速度都为每秒1个单位长度.设移动时间为t秒(). (1)求直线的解析式. (2)设△PCQ的面积为S.请求出S关于t的函数关系式. (3)试探究:当t为何值时.△PCQ为等腰三角形? 4029． 如图.在平面直角坐标系中.直线与交于点.分别交轴于点和点.点是直线上的一个动点． (1)求点的坐标． (2)当为等腰三角形时.求点的坐标． (3)在直线上是否存在点.使得以点为顶点的四边形是平行四边形?如果存在.直线写出的值,如果不存在.请说明理由． 29．解:(1)在中.当时.. .点的坐标为．·········································································· 1分 在中.当时..点的坐标为(4.0)．·· 2分 由题意.得解得 点的坐标为．····················································································· 3分 (2)当为等腰三角形时.有以下三种情况.如图(1)．设动点的坐标为． 由(1).得.． ①当时.过点作轴.垂足为点.则． ． .点的坐标为．················································· 4分 ②当时.过点作轴.垂足为点.则． .. ． 解.得．此时.． 点的坐标为．·············································································· 6分 ③当.或时.同理可得．····················· 9分 由此可得点的坐标分别为． 评分说明:符合条件的点有4个.正确求出1个点的坐标得1分.2个点的坐标得3分.3个点的坐标得5分.4个点的坐标得满分,与所求点的顺序无关． (3)存在．以点为顶点的四边形是平行四边形有以下三种情形.如图(2)． ①当四边形为平行四边形时.．··········································· 10分 ②当四边形为平行四边形时.．············································ 11分 ③当四边形为平行四边形时.．········································ 12分 4125. 某县社会主义新农村建设办公室.为了解决该县甲.乙两村和一所中学长期存在的饮水困难问题.想在这三个地方的其中一处建一所供水站.由供水站直接铺设管道到另外两处. 如图.甲.乙两村坐落在夹角为30°的两条公路的AB段和CD段.点M表示这所中学.点B在点M的北偏西30°的3km处.点A在点M的正西方向.点D在点M的南偏西60°的km处. 为使供水站铺设到另两处的管道长度之和最短.现有如下三种方案: 方案一:供水站建在点M处.请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值, 方案二:供水站建在乙村.甲村要求管道铺设到A处.请你在图①中.画出铺设到点A和点M处的管道长度之和最小的线路图.并求其最小值, 方案三:供水站建在甲村.请你在图②中.画出铺设到乙村某处和点M处的管道长度之和最小的线路图.并求其最小值. 综上.你认为把供水站建在何处.所需铺设的管道最短? 25.解:方案一:由题意可得:MB⊥OB. ∴点M到甲村的最短距离为MB.------- ∵点M到乙村的最短距离为MD. ∴将供水站建在点M处时.管道沿MD.MB线路铺设的长度之和最小. 即最小值为MB+MD=3+ 方案二:如图①.作点M关于射线OE的对称点M′.则MM′＝2ME. 连接AM′交OE于点P.PE∥AM.PE＝. ∵AM＝2BM＝6.∴PE＝3 ------- 在Rt△DME中.∵DE＝DM·sin60°＝×＝3.ME＝＝×. ∴PE＝DE.∴ P点与E点重合.即AM′过D点.---- 在线段CD上任取一点P′.连接P′A.P′M.P′M′. 则P′M＝P′M′.∵A P′+P′M′＞AM′. ∴把供水站建在乙村的D点处.管道沿DA.DM线路铺设的长度之和最小. 即最小值为AD+DM＝AM′＝--- 方案三:作点M关于射线OF的对称点M′.作M′N⊥OE于N点.交OF于点G. 交AM于点H.连接GM.则GM＝GM′ ∴M′N为点M′到OE的最短距离.即M′N＝GM+GN 在Rt△M′HM中.∠MM′N＝30°.MM′＝6. ∴MH＝3.∴NE＝MH＝3 ∵DE＝3.∴N.D两点重合.即M′N过D点. 在Rt△M′DM中.DM＝.∴M′D＝---- 在线段AB上任取一点G′.过G′作G′N′⊥OE于N′点. 连接G′M′.G′M. 显然G′M+G′N′＝G′M′+G′N′＞M′D ∴把供水站建在甲村的G处.管道沿GM.GD 线路铺设的长度之和最小.即最小值为 GM+GD＝M′D＝. - 综上.∵3+＜. ∴供水站建在M处.所需铺设的管道长度最短. ---- 【查看更多】

     

    题目列表(包括答案和解析)

    已知n是正整数，pn(xn,yn)是反比例函数y=的图象上的一列点，其中x1=1，x2=2，…，xn=n,记

    T1= x1y2，T2= x2y3，…，T8= x8y9；若T1=1，则T1 •T2 • … •T8的值是__________.（08衢州卷第16题改编）

    查看答案和解析>>

    2、本卷第17～25题的9道题中，每道题所赋分数（注：分值依次为6，7，7，8，8，8，9，9，10）的众数和中位数分别是（　　）

    查看答案和解析>>

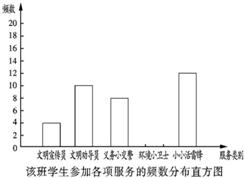    20、在我市实施“文明伴我行”期间，我校组织学生开展“走出校门，服务社会”的公益活动．八年级一班小浩根据本班同学参加这次活动的情况，制作了如下的统计图表：
    该班学生参加各项服务的频数、频率统计表
    服务类别 频数 频率
    文明宣传员 4 0.08
    文明劝导员 10
    义务小交警 8 0.16
    环境小卫士 0.32
    小小活雷锋 12 0.24
    请根据上面的统计图表，解答下列问题：
    （1）该班参加这次公益活动的学生共有
    50
    名；
    （2）请补全频数、频率统计表和频数分布直方图；
    （3）若八年级共有900名学生报名参加了这次公益活动，试估计参加文明劝导的学生人数．

    查看答案和解析>>

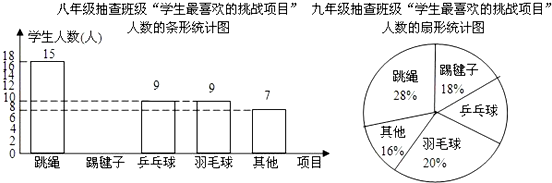
    19、某校初三年级一班班长调查了本班50名同学的身高，把所得的数据进行整理分组，画出频率分布直方图的一部分（如下图所示），已知图中从左到右的第一、二、三、四组的频率依次是：0.08，0.2，0.4，0.24
    ①求出第五组的频数；
    ②请将频率分布直方图补充完整．

    查看答案和解析>>

    某校欲举办“校园吉尼斯挑战赛”，为此该校在三个年级中各随机抽取一个班级进行了一次“你最喜欢的挑战项目”的问卷调查，每名学生都选了一项、已知被调查的三个年级的学生人数均为50人，根据收集到的数据，绘制成如下统计图表（不完整）：
    七年级抽查班级“学生最喜欢的挑战项目”人数统计
    项目 跳绳 踢毽子 乒乓球 羽毛球 其他
    人数（人）   14 10 8 6
    精英家教网
    根据统计图表中的信息，解答下列问题：
    （1）在本次随机调查中，七年级抽查班级中喜欢“跳绳”项目的学生有
     
    人，九年级抽查班级中喜欢“乒乓球”项目的学生人数占本班人数的百分比为
     
    ；
    （2）请将条形统计图补充完整；（温馨提示：请画在答题卷相对应的上）
    （3）若该校共有900名学生（三个年级的学生人数都相等），请你估计该校喜欢“羽毛球”项目的学生总人数．

    查看答案和解析>>


    同步练习册答案