练习册

  • 练习册
  • 试题
    24．如图.直角坐标系中.已知两点.点在第一象限且为正三角形.的外接圆交轴的正半轴于点.过点的圆的切线交轴于点． (1)求两点的坐标, (2)求直线的函数解析式, (3)设分别是线段上的两个动点.且平分四边形的周长． 试探究:的最大面积? 24．(1).． 作于. 为正三角形. .． ． 连... ． ． (2).是圆的直径. 又是圆的切线.． .． ． 设直线的函数解析式为. 则.解得． 直线的函数解析式为． (3).... 四边形的周长． 设.的面积为. 则.． ． 当时.． 点分别在线段上. .解得． 满足. 的最大面积为． 5524. 如图1.在平面直角坐标系中.己知ΔAOB是等边三角形.点A的坐标是(0.4).点B在第一象限.点P是x轴上的一个动点.连结AP.并把ΔAOP绕着点A按逆时针方向旋转.使边AO与AB重合.得到ΔABD.(1)求直线AB的解析式,(2)当点P运动到点(.0)时.求此时DP的长及点D的坐标,(3)是否存在点P.使ΔOPD的面积等于.若存在.请求出符合条件的点P的坐标,若不存在.请说明理由. 5624．如图.在平面直角坐标系中.已知点坐标为(2.4).直线与轴相交于点.连结.抛物线从点沿方向平移.与直线交于点.顶点到点时停止移动． (1)求线段所在直线的函数解析式, (2)设抛物线顶点的横坐标为, ①用的代数式表示点的坐标, ②当为何值时.线段最短, (3)当线段最短时.相应的抛物线上是否存在点.使△ 的面积与△的面积相等.若存在.请求出点的坐标,若 不存在.请说明理由． 24． 解:(1)设所在直线的函数解析式为. ∵(2.4). ∴, , ∴所在直线的函数解析式为.------------- (2)①∵顶点M的横坐标为.且在线段上移动. ∴(0≤≤2). ∴顶点的坐标为(,). ∴抛物线函数解析式为. ∴当时.(0≤≤2). ∴点的坐标是(2.).------------- ② ∵==. 又∵0≤≤2. ∴当时.PB最短. ----------------- (3)当线段最短时.此时抛物线的解析式为.----- 假设在抛物线上存在点.使. 设点的坐标为(.). ①当点落在直线的下方时.过作直线//.交轴于点. ∵.. ∴.∴.∴点的坐标是(0.). ∵点的坐标是(2.3).∴直线的函数解析式为. ∵.∴点落在直线上. ∴=. 解得.即点(2.3). ∴点与点重合. ∴此时抛物线上不存在点.使△与 △的面积相等.--------- ②当点落在直线的上方时. 作点关于点的对称称点.过作直线//.交轴于点. ∵.∴.∴.的坐标分别是. ∴直线函数解析式为. ∵.∴点落在直线上. ∴=. 解得:.. 代入.得.. ∴此时抛物线上存在点. 使△与△的面积相等. ------------- 综上所述.抛物线上存在点. 使△与△的面积相等. 5724.已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示.四个顶点的坐标分别为O.B(8.).C(0.).点T在线段OA上.将纸片折叠.使点A落在射线AB上.折痕经过点T.折痕TP与射线AB交于点P.设点T的横坐标为t.折叠后纸片重叠部分的面积为S, (1)求∠OAB的度数.并求当点A′在线段AB上时.S关于t的函数关系式, (2)当纸片重叠部分的图形是四边形时.求t的取值范围, (3)S存在最大值吗?若存在.求出这个最大值.并求此时t的值,若不存在.请说明理由. 24. 解:(1) ∵A.B两点的坐标分别是A和B(8.). ∴. ∴ 当点A´在线段AB上时.∵.TA=TA´. ∴△A´TA是等边三角形.且. ∴.. A´ y E ∴. x O C T P B A 当A´与B重合时.AT=AB=. 所以此时. (2)当点A´在线段AB的延长线.且点P在线段AB上时. 纸片重叠部分的图形是四边形.其中E是TA´与CB的交点). A´ y x 当点P与B重合时.AT=2AB=8.点T的坐标是(2.0) 又由(1)中求得当A´与B重合时.T的坐标是(6.0) P B E 所以当纸片重叠部分的图形是四边形时.. F C (3)S存在最大值 A T O 1当时.. 在对称轴t=10的左边.S的值随着t的增大而减小. ∴当t=6时.S的值最大是. 2当时.由图1.重叠部分的面积 ∵△A´EB的高是. ∴ 当t=2时.S的值最大是, 3当.即当点A´和点P都在线段AB的延长线是(如图2.其中E是TA´与CB的交点.F是TP与CB的交点). ∵.四边形ETAB是等腰形.∴EF=ET=AB=4. ∴ 综上所述.S的最大值是.此时t的值是. 5824．将一矩形纸片放在平面直角坐标系中...．动点从点出发以每秒1个单位长的速度沿向终点运动.运动秒时.动点从点出发以相等的速度沿向终点运动．当其中一点到达终点时.另一点也停止运动．设点的运动时间为(秒)． (1)用含的代数式表示, (2)当时.如图1.将沿翻折.点恰好落在边上的点处.求点的坐标, (3)连结.将沿翻折.得到.如图2．问:与能否平行?与能否垂直?若能.求出相应的值,若不能.说明理由． 24． 解:(1).． (2)当时.过点作.交于.如图1. 则.. .． (3)①能与平行． 若.如图2.则. 即..而. ． ②不能与垂直． 若.延长交于.如图3. 则． ． ． 又.. . .而. 不存在． 【查看更多】

     

    题目列表(包括答案和解析)

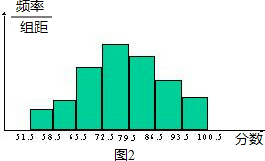
    19、某校课外活动小组为了解本校九年级学生的睡眠时间情况，对学校若干名九年级学生的睡眠时间进行了抽查，将所得数据整理后，画出了频率分布直方图的一部分（如图所示）．根据全班睡眠时间统计共分为六个小组，图中从左至右前五个小组的频率分别是0.04，0.08，0.24，0.28，0.24，第二小组的频数为4．请回答：
    （1）这次被抽查的学生人数是多少？并补全频率分布直方图．
    （2）被抽查的学生中，睡眠时间在哪个范围内的人数最多？这一范围内的人数是多少？
    （3）如果该学校有900名九年级学生，若合理睡眠时间范围为7≤t＜9，那么请你估计一下这个学校九年级学生中睡眠时间在此范围内的人数是多少？

    查看答案和解析>>

    24、下表是中国足球甲级联赛 2005一2006赛季积分榜的一部分（前三名）：
    名次 球 队 场次 胜 平 负 进球 失球 净胜球 积分
    1 河南建业 24 1 38 13 25 59
    2 浙江绿城 24 17 4 3 41 18 23
    3 广州医药 24 15 3 6 45 25 48
    备   注 胜一场得3分，平一场得1分，负一场得0分
    请你根据表中的数据回答下列问题：
    （1）浙江绿城队最后的积分是
    55
    分，广州医药队的净胜球是
    20
    个．
    （2）请你计算河南建业队在本赛季胜、平各多少场？
    （3）失球数的多少可以用来衡量一个球队的防守质量，根据表中的失球数，请你分析这三个队中哪个队的防守质量相对较差？你认为该球队下赛季应引进什么位置的球员，才能有效地提高防守质量？

    查看答案和解析>>

    在一次环保知识测试中，三年一班的两名同学根据班级成绩（分数为整数）分别绘制了不同的频率分布直方图，如图1、2，已知图1从左到右每个小组的频率分别为0.04、0.08、0.24、0.32、0.20、0.12，其中68.5～76.5小组的频数为12；图2从左到右每个小组的频数之比为1：2：4：7：6：3：2，请结合条件和频率分布直方图回答下列问题：
    （1）三年一班参加测试的人数是多少？
    （2）若这次测试的成绩80分以上（含80分）为优秀，则优秀率是多少？
    （3）若这次测试的成绩60分以上（含60分0为及格，则及格率是多少？
    精英家教网精英家教网

    查看答案和解析>>

     

    ①（2010四川眉山）解方程：

    ②（2010浙江嘉兴）解方程：．

     

    查看答案和解析>>

    某校课外活动小组为了解本校九年级学生的睡眠时间情况，对学校若干名九年级学生的睡眠时间进行了抽查，将所得数据整理后，画出了频数分布直方图的一部分，如图，已知图中从左至右前5个小组的频率分别是0.04，0.08，0.24，0.28，0.24，第二小组的频数为4．

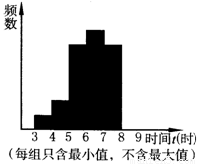
    请回答下列问题：

    （1）这次被抽查的学生人数是多少？并请补全频数分布直方图．

    （2）被抽查的学生中，睡眠时间在哪个范围内的人数最多？这一范围内的人数是多少？

    （3）如果该学校有900名九年级学生，若合理睡眠时间范围为7≤t<9，那么请你估计一下这个学校九年级学生中睡眠时间在此范围内的人数是多少？

     

    查看答案和解析>>


    同步练习册答案