在平面直角坐标系中给定以下五个点． (1)请从五点中任选三点.求一条以平行于轴的直线为对称轴的抛物线的解析式, (2)求该抛物线的顶点坐标和对称轴.并画出草图, (3)已知点在抛物线的对称轴——青夏教育精英家教网—

在平面直角坐标系中给定以下五个点． (1)请从五点中任选三点.求一条以平行于轴的直线为对称轴的抛物线的解析式, (2)求该抛物线的顶点坐标和对称轴.并画出草图, (3)已知点在抛物线的对称轴上.直线过点且垂直于对称轴．验证:以为圆心.为半径的圆与直线相切．请你进一步验证.以抛物线上的点为圆心为半径的圆也与直线相切．由此你能猜想到怎样的结论． 25．解:(1)设抛物线的解析式为. 且过点. 由在H ．则．········································································································ 得方程组. 解得．抛物线的解析式为················ (2)由············· 得顶点坐标为.对称轴为．·········· (3)①连结.过点作直线的垂线.垂足为. 则．在中... . . 以点为圆心.为半径的与直线相切．····························· ②连结过点作直线的垂线.垂足为．过点作垂足为. 则．在中..．．以点为圆心为半径的与直线相切．································ ③以抛物线上任意一点为圆心.以为半径的圆与直线相切．····· 【查看更多】

题目列表(包括答案和解析)

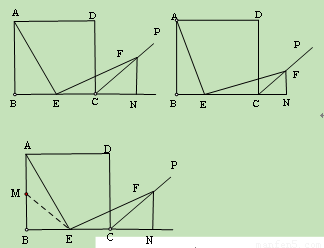
（2011内蒙古赤峰，25，14分）如图（图1、图2），四边形ABCD是边长为4的正方形，点E在线段BC上，∠AEF=90°，且EF交正方形外角平分线CP于点F，FN⊥BC，交BC的延长线于点N。

（1）若点E是BC的中点（如图1），AE与EF相等吗？为什么？

（2）点E在BC间运动时（如图2），设BE=x, △ECF的面积为y。

①求y与x的函数关系式；

②当x取何值时，y有最大值，并求出这个最大值。

查看答案和解析>>

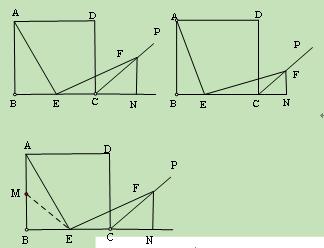
（2011内蒙古赤峰，25，14分）如图（图1、图2），四边形ABCD是边长为4的正方形，点E在线段BC上，∠AEF=90°，且EF交正方形外角平分线CP于点F，FN⊥BC，交BC的延长线于点N。
（1）若点E是BC的中点（如图1），AE与EF相等吗？为什么？
（2）点E在BC间运动时（如图2），设BE=x,△ECF的面积为y。
①求y与x的函数关系式；
②当x取何值时，y有最大值，并求出这个最大值。