如图，正比例函数与反比例函数相交于A、B点，已知点A的坐标为（4，n），BD⊥x轴于点D，且S_△BDO=4。过点A的一次函数与反比例函数的图像交于另一点C，与x轴交于点E（5，0）。

（1）求正比例函数、反比例函数和一次函数的解析式；

（2）结合图像，求出当时x的取值范围。

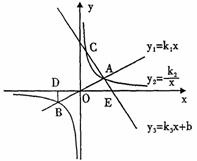
         第26题

已知抛物线M：y = -x²+2mx+n（m，n为常数，且m> 0，n>0）的顶点为A，与y轴交于点C；抛物线N与抛物线M关于y轴对称，其顶点为B，连结AC，BC，AB．

问抛物线M上是否存在点P，使得四边形ABCP为菱形？如果存在，请求出m的值；如果不存在，请说明理由．

说明：⑴如果你反复探索,没有解决问题, 请写出探索过程(要求至少写3步)；

⑵在你完成⑴之后,可以从①、②中选取一个条件，完成解答（选取①得7分；选取②得10分）．

①；②．

附加题: 若将26题中“抛物线M：y= -x²+2mx+n（m，n为常数，且m> 0，n>0） ”改为“抛物线M：y= ax²+2mx+n（m，n为常数，且m≠ 0,a≠0, n>0） ”，其他条件不变, 探究 26题中问题．

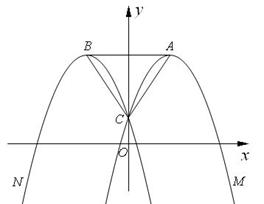
已知抛物线M：y = -x²+2mx+n（m，n为常数，且m> 0，n>0）的顶点为A，与y轴交于点C；抛物线N与抛物线M关于y轴对称，其顶点为B，连结AC，BC，AB．

问抛物线M上是否存在点P，使得四边形ABCP为菱形？如果存在，请求出m的值；如果不存在，请说明理由．

说明：⑴如果你反复探索,没有解决问题, 请写出探索过程(要求至少写3步)；

⑵在你完成⑴之后,可以从①、②中选取一个条件，完成解答（选取①得7分；选取②得10分）．

①；②．

附加题: 若将26题中“抛物线M：y= -x²+2mx+n（m，n为常数，且m> 0，n>0） ”改为“抛物线M：y= ax²+2mx+n（m，n为常数，且m≠ 0,a≠0, n>0） ”，其他条件不变, 探究 26题中问题．