
题目列表(包括答案和解析)
已知函数f(x)=alnx-x2+1.
(1)若曲线y=f(x)在x=1处的切线方程为4x-y+b=0,求实数a和b的值;
(2)若a<0,且对任意x1、x2∈(0,+∞),都|f(x1)-f(x2)|≥|x1-x2|,求a的取值范围.
【解析】第一问中利用f′(x)= -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
由已知得a-2=4,2-a=b,所以a=6,b=-4.
第二问中,利用当a<0时,f′(x)<0,∴f(x)在(0,+∞)上是减函数,
不妨设0<x1≤x2,则|f(x1)-f(x2)|=f(x1)-f(x2),|x1-x2|=x2-x1,
∴|f(x1)-f(x2)|≥|x1-x2|等价于f(x1)-f(x2)≥x2-x1,
即f(x1)+x1≥f(x2)+x2,结合构造函数和导数的知识来解得。
(1)f′(x)= -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
由已知得a-2=4,2-a=b,所以a=6,b=-4.
(2)当a<0时,f′(x)<0,∴f(x)在(0,+∞)上是减函数,
不妨设0<x1≤x2,则|f(x1)-f(x2)|=f(x1)-f(x2),|x1-x2|=x2-x1,
∴|f(x1)-f(x2)|≥|x1-x2|等价于f(x1)-f(x2)≥x2-x1,即f(x1)+x1≥f(x2)+x2,
令g(x)=f(x)+x=alnx-x2+x+1,g(x)在(0,+∞)上是减函数,
∵g′(x)= -2x+1=
-2x+1= (x>0),
(x>0),
∴-2x2+x+a≤0在x>0时恒成立,
∴1+8a≤0,a≤- ,又a<0,
,又a<0,
∴a的取值范围是
如果关于![]() 的不等式
的不等式![]() 的正整数解是
的正整数解是![]() ,那么实数
,那么实数![]() 的取值范围是( ).
的取值范围是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
设 ,
,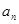 表示关于
表示关于 的不等式
的不等式 的正整数解的个数,则数列
的正整数解的个数,则数列 的通项公式
的通项公式 .
.
若关于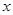 的不等式
的不等式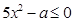 的正整数解有且只有1,2,3,则实数
的正整数解有且只有1,2,3,则实数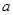 的取值范围是
的取值范围是
A.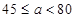 B.
B.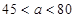 C.
C.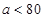 D.
D.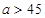
如果关于 的不等式
的不等式 的正整数解是
的正整数解是 ,4,那么实数
,4,那么实数 的取值范围是( )
的取值范围是( )
A.80≤ <125
B.80<
<125
B.80< <125 C.
<125 C. D.
D. >125
>125
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com