
题目列表(包括答案和解析)
A.所有正三角形 B.数学课本中的所有习题
C.2006年高考试卷中的所有难题 D.所有无理数
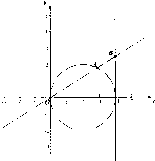 已知点A(x1,y1)在圆(x-2)2+y2=4上运动,点A不与(0,0)重合,点B(4,y0)在直线x=4上运动,动点M(x,y)满足
已知点A(x1,y1)在圆(x-2)2+y2=4上运动,点A不与(0,0)重合,点B(4,y0)在直线x=4上运动,动点M(x,y)满足| OM |
| OB |
| OM |
| AB |
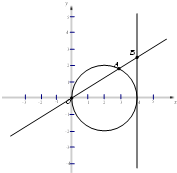 (2011•南汇区二模)已知动直线y=kx交圆(x-2)2+y2=4于坐标原点O和点A,交直线x=4于点B,若动点M满足
(2011•南汇区二模)已知动直线y=kx交圆(x-2)2+y2=4于坐标原点O和点A,交直线x=4于点B,若动点M满足| OM |
| AB |
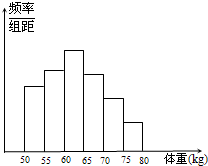 某校高三年级学生高考报名体检时,得到一组男生体重(单位:kg)数据,进行整理后分成六组,并绘制频率分布直方图(如图所示).已知图中从左到右第一、第六小组的频率分别为0.16、0.07,第一、第二、第三小组的频率成等比数列,第三、第四、第五、第六小组的频率成等差数列,且第三小组的频数为200,则该校高三年级的男生总数为
某校高三年级学生高考报名体检时,得到一组男生体重(单位:kg)数据,进行整理后分成六组,并绘制频率分布直方图(如图所示).已知图中从左到右第一、第六小组的频率分别为0.16、0.07,第一、第二、第三小组的频率成等比数列,第三、第四、第五、第六小组的频率成等差数列,且第三小组的频数为200,则该校高三年级的男生总数为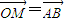 ,动点M的轨迹C的方程为F(x,y)=0.
,动点M的轨迹C的方程为F(x,y)=0.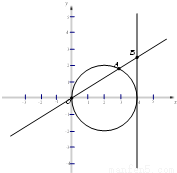
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com