党的十七大报告提出“要增强发展的协调性，努力实现国民经济又好又快发展”。下面做法符合这一要求的是                                                    （   ）

①淘汰落后产能，实施节能减排        ②优化产业结构，促进经济发展方式转变

③提高自主创新能力，建设创新型国家  ④把提高经济增长速度放在工作的首位

下列命题：
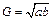①是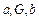成等比数列的充分不必要条件；
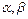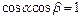②若角满足，则；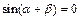
③若不等式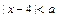的解集非空，则必有；
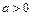④“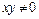”是指 “”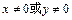
⑤命题“存在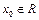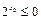，”的否定是“对任意的，”.
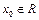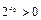其中正确的命题的序号是（把你认为正确的命题的序号都填上）.

下列命题：

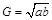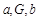①是成等比数列的充分不必要条件；

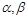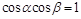②若角满足，则；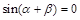

③若不等式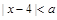的解集非空，则必有；

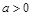④“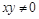”是指 “”

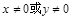⑤命题“存在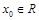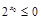，”的否定是“对任意的，”.

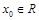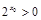其中正确的命题的序号是（把你认为正确的命题的序号都填上）.

     (1)分别对男、女学生抽取一个容量相同的样本,样本容量可在40—50之间选择.若高一男、女学生各抽取的人数定为18人,那么高二、高三男、女学生的人数各应定为多少?

     (2)上述描样采用的是哪种抽样方法?所得男、女学生的样本容量是多少?

     (3)如果按照上述抽样方法采集的各样本数据如下表(单位:分)

    求相应于男生标本的平均数_男,标准差s_男,相应于女生样本的平均均数_女,标准差s_女,和男、女学生全体组成的新样本的平均数x、标准差s.根据以上结果作出估计分析.