
题目列表(包括答案和解析)
该空间几何体为一圆柱和一四棱锥组成的,圆柱的底面半径为1,高为2,体积为![]() ,四棱锥的底面边长为
,四棱锥的底面边长为![]() ,高为
,高为![]() ,所以体积为
,所以体积为![]()
所以该几何体的体积为![]() .
.
答案:C
【命题立意】:本题考查了立体几何中的空间想象能力,
由三视图能够想象得到空间的立体图,并能准确地计算出
几何体的体积.
已知曲线 的参数方程是
的参数方程是 (
( 是参数),以坐标原点为极点,
是参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 :的极坐标方程是
:的极坐标方程是 =2,正方形ABCD的顶点都在
=2,正方形ABCD的顶点都在 上,且A,B,C,D依逆时针次序排列,点A的极坐标为(2,
上,且A,B,C,D依逆时针次序排列,点A的极坐标为(2, ).
).
(Ⅰ)求点A,B,C,D的直角坐标;
(Ⅱ)设P为 上任意一点,求
上任意一点,求 的取值范围.
的取值范围.
【命题意图】本题考查了参数方程与极坐标,是容易题型.
【解析】(Ⅰ)由已知可得 ,
, ,
,
 ,
, ,
,
即A(1, ),B(-
),B(- ,1),C(―1,―
,1),C(―1,― ),D(
),D( ,-1),
,-1),
(Ⅱ)设 ,令
,令 =
= ,
,
则 =
= =
= ,
,
∵ ,∴
,∴ 的取值范围是[32,52]
的取值范围是[32,52]
已知函数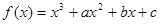 ,曲线
,曲线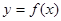 在点x=1处的切线为
在点x=1处的切线为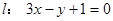 ,若
,若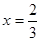 时,
时,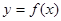 有极值。
有极值。
(1)求 的值;
(2)求
的值;
(2)求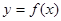 在
在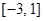 上的最大值和最小值。
上的最大值和最小值。
【解析】本试题主要考查了导数的几何意义的运用,以及运用导数在研究函数的极值和最值的问题。体现了导数的工具性的作用。
已知动点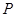 与平面上两定点
与平面上两定点 连线的斜率的积为定值
连线的斜率的积为定值 .
.
(1)试求动点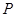 的轨迹方程
的轨迹方程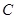 ;
;
(2)设直线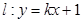 与曲线
与曲线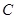 交于M.N两点,当
交于M.N两点,当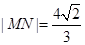 时,求直线
时,求直线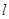 的方程.
的方程.
【解析】本试题主要是考查了轨迹方程的求解以及直线与椭圆位置关系的运用。
已知函数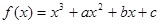 ,曲线
,曲线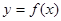 在点x=1处的切线为
在点x=1处的切线为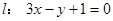 ,若
,若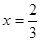 时,
时,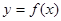 有极值。
有极值。
(1)求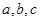 的值;
(2)求
的值;
(2)求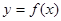 在
在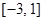 上的最大值和最小值。
上的最大值和最小值。
【解析】本试题主要考查了导数的几何意义的运用,以及运用导数在研究函数的极值和最值的问题。体现了导数的工具性的作用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com