练习册

  • 练习册
  • 试题
    已知△ABC的角A.B.C所对的边分别是a.b.c.设向量m＝(a.b).n＝(sinB.sinA).p＝(b-2.a-2). (1)若m∥n.求证:△ABC为等腰三角形, (2)若m⊥p.边长c＝2.角C＝.求△ABC的面积. 解:(1)证明:∵m∥n.∴asinA＝bsinB. 即a·＝b·. 其中R是△ABC外接圆半径.∴a＝b. ∴△ABC为等腰三角形. (2)由题意可知m·p＝0.即a(b-2)+b(a-2)＝0. ∴a+b＝ab. 由余弦定理可知.4＝a2+b2-ab＝(a+b)2-3ab. 即(ab)2-3ab-4＝0. ∴ab＝4(舍去ab＝-1). ∴S＝absinC＝×4×sin＝. 【查看更多】

     

    题目列表(包括答案和解析)

    已知△ABC的角A、B、C所对的边分别是a、b、c，设向量
    m
    =(a，b)    ，
    n
    =(sinB，sinA)    ，
    p
    =(b-2，a-2)    ．
    （1）若
    m
    ∥
    n
    ，求证：△ABC为等腰三角形；
    （2）若
    m
    ⊥
    p
    ，边长c=2，角C=
    π
    3
    ，求△ABC的面积．

    查看答案和解析>>

    已知△ABC的角A、B、C所对的边分别是a、b、c，设向量
    m
    =（a，b），
    n
    =（sinA，cosB），
    P
    =（1，1）．
    （I）若
    m
    ∥
    n
    ，求角B的大小：
    （Ⅱ）若
    m
    •
    p
    =4，边长c=2，角c=
    π
    3
    求△ABC的面积．

    查看答案和解析>>

    已知ΔABC的角A、B、C所对的边分别是a、b、c，设向量，

    　　， .

    （1）若//，求证：ΔABC为等腰三角形；     

    (2)若⊥，边长c = 2，角C = ，求ΔABC的面积 .

    查看答案和解析>>

    已知ΔABC的角A、B、C所对的边分别是a、b、c，设向量，

    　　， .（1）若//，判断ΔABC的形状并给出证明；  （2）若⊥，边长c = 2，角C = ，求ΔABC的面积 .

    查看答案和解析>>

    已知ΔABC的角A、B、C所对的边分别是a、b、c，设向量，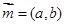
    　　， .
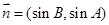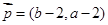    （1）若//，求证：ΔABC为等腰三角形；    
    (2)若⊥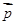，边长c = 2，角C = 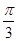，求ΔABC的面积 .

    查看答案和解析>>


    同步练习册答案